Towards a Microscopic Traffic Simulation of All of Switzerland

Bryan Raney1 - Andreas Voellmy1 - Nurhan Cetin1 - Milenko Vrtic2 - Kai Nagel1

Dept. of Computer Science, ETH Zentrum IFW B27.1,
CH-8092 Zürich, Switzerland - Inst. for Transportation Planning IVT, ETH Hönggerberg HIL F32.3,
CH-8093 Zürich, Switzerland

Zusammenfassung:

Multi-agent transportation simulations are rule-based. The fact that such simulations do not vectorize means that the recent move to distributed computing architectures results in an explosion of computing capabilities of multi-agent simulations. This paper describes the general modules which are necessary for transportation planning simulations, reports the status of an implementation of such a simulation for all of Switzerland, and gives computational performance numbers.

Keywords: Traffic Simulation, Transportation Planning, TRANSIMS, parallel computing

Introduction

Human transportation has physical, engineering, and socio-economic aspects. This last aspect means that any simulation of human transportation systems will include elements of adaptation, learning, and individual planning. In terms of computerization, these aspects can be much better described by rules which are applied to individual entities than by equations which are applied to aggregated fields. This means that a rule-based multi-agent simulation is a promising method for transportation simulations (and for socio-economic simulations in general). By a ``multi-agent'' simulation we mean a microscopic simulation that models the behavior of each traveler, or agent, within the transportation system as an individual, rather than aggregating their behavior in some way. These agents are intelligent, which means that they have strategic, long-term goals. They also have internal representations of the world around them which they use to reach these goals. Adding the term ``rule-based'' indicates that the behavior of the agents is determined by sets of rules instead of equations. Thus, a rule-based multi-agent simulation of a transportation system will apply to each agent individually. This means such a simulation differs significantly from a microscopic simulation of, say, molecular dynamics, because unlike molecules, two ``traveler'' particles (agents) in identical situations within a transportation simulation will in general make different decisions.

Such rule-based multi-agent simulations run well on current workstations and they can be distributed on parallel computers of the type ``networks of coupled workstations.'' Since these simulations do not vectorize, this means that the jump in computational capability over the last decade has had a greater impact on the performance of multi-agent simulations than for, say, computational fluid-dynamics, which also worked well in vector-based computational environments. In practical terms, this means that we are now able to run microscopic simulations of large metropolitan regions with more than 10 million travelers. These simulations are even fast enough to run them many times in sequence, which is necessary to emulate the day-to-day dynamics of human learning, for example in reaction to congestion.

In order to demonstrate this capability and also in order to gain practical experience with such a simulation system, we are currently implementing a 24-hour microscopic transportation simulation of all of Switzerland. Switzerland has 7.2 million inhabitants. Assuming 3 to 3.5 trips per person per day, this will result in about 20-25 million trips. This number includes pedestrian trips (like walking to lunch), trips by public transit, freight traffic, etc. The number of car trips on a typical weekday in Switzerland is currently about 5 million (see [1] for where the data comes from). The goal of this study is twofold:

• Investigate if it is possible to make TRANSIMS realistic enough to be useful for such a scenario, and how difficult this is.

• Investigate the computational challenges and how they can be overcome.

This paper gives a short report on the current status. Section 2 describes the simulation modules and how they were used for the purposes of this study. Section 3 describes the input data, i.e. the underlying network and the demand generation. Besides ``normal'' demand, we also describe one where 50000 travelers travel from random starting points within Switzerland to the Ticino, which is the southern part of Switzerland. We use this second scenario as a plausibility test for routing and feedback. This is followed by Sect. 4, which describes some results, and by a Summary.

Simulation Modules

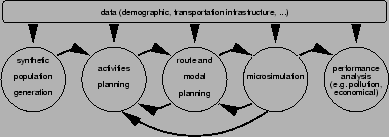
Traffic simulations for transportation planning typically consist of the following modules (Fig. 1):

• Population generation. Demographic data is disaggregated so that one obtains individual households and individual household members, with certain characteristics, such as a street address, car ownership, or household income [2]. - This module is not used for our current investigations but will be used in future.

• Activities generation. For each individual, a set of activities (home, going shopping, going to work, etc.) and activity locations for a day is generated [3,4]. - This module is not used in our current investigations but will be used in future.

• Modal and route choice. For each individual, modes and routes are generated that connect activities at different locations [5].

• Traffic micro-simulation. Up to here, all individuals have made plans about their behavior. The traffic micro-simulation executes all those plans simultaneously [6]. In particular, we now obtain the result of interactions between the plans - for example congestion.

• Feedback. In addition, such an approach needs to make the modules consistent with each other. For example, plans depend on congestion, but congestion depends on plans. A widely accepted method to resolve this is systematic relaxation [7] - that is, make preliminary plans, run the traffic micro-simulation, adapt the plans, run the traffic micro-simulation again, etc., until consistency between modules is reached. The method is somewhat similar to a standard relaxation technique in numerical analysis.

This modularization has in fact been used for a long time; the main difference is that it is now feasible to make all modules completely microscopic, i.e. each traveler is individually represented in all modules.

Abbildung 1: TRANSIMS modules

Routing

Travelers/vehicles need to compute the sequence of links that they are taking through the network. A typical way to obtain such paths is to use a shortest path Dijkstra algorithm [5]. This algorithm uses as input the individual link travel times plus the starting and ending point of a trip, and generates as output the fastest path.

It is relatively straightforward to make the costs (link travel times) time dependent, meaning that the algorithm can include the effect that congestion is time-dependent: Trips starting at one time of the day will encounter different delay patterns than trips starting at another time of the day. Link travel times are fed back from the micro-simulation in 15-min time bins, and the router finds the fastest route based on these 15-min time bins. Apart from relatively small and essential technical details, the implementation of such an algorithm is fairly standard [5]. It is possible to include public transportation into the routing [8]; in our current work, we look at car traffic only.

Micro-Simulation

We use two different micro-simulations, one being the micro-simulation of the TRANSIMS [9] project and the other one being a so-called queue micro-simulation that we also use for computational performance testing. The TRANSIMS micro-simulation is a complex package with many rules and details. In order to speed up the computation, the driving rules are based on the cellular automaton (CA) method [10] with additional rules for lane changing and protected as well as unprotected turns [6]. The result is, within the limits of the capabilities of a CA, a virtual reality traffic simulation. Note that besides the usual traffic dynamics, vehicles also follow routes as specified above. This means, for example, that vehicles need to change lanes in order to be in one of the allowed lanes for the desired turning movement. Vehicles which fail to do this because of too much traffic are removed from the simulation.

The queue simulation [11,12] is simpler in its traffic dynamics capabilities. Streets are essentially represented as FIFO (first-in first-out) queues, with the additional restrictions that (1) vehicles have to remain for a certain time on the link, corresponding to free speed travel time; and that (2) there is a link storage capacity and once that is exhausted, no more vehicles can enter the link.

A major advantage of the queue simulation, besides its simplicity, is that it can run directly off the data typically available for transportation planning purposes. For the more complicated TRANSIMS micro-simulation, a lot of data conversion and additional assumptions have to be made.

Feedback

As mentioned above, plans (such as routes) and congestion need to be made consistent. This is achieved via a relaxation technique:

1. Initially, the system generates a set of routes based on free speed travel times.

2. The traffic simulation is run with these routes.

3. 10% of the population is gets new routes, which are based on the link travel times of the last traffic simulation.

4. This cycle (i.e. steps (2) and (3)) is run for 50 times; earlier investigations have shown that this is more than enough to reach relaxation [13].

Note that this implies that routes are fixed during the traffic simulation and can only be changed between iteration runs. Work is under way to improve this situation, i.e. to allow online re-planning.

Input Data and Scenarios

The input data consists of two parts: the street network, and the demand.

The Street Network

The network that is used was originally developed for the Swiss regional planning authority (Bundesamt für Raumentwicklung). It has since been updated, corrected and calibrated by Vrtic at the IVT. The network has the fairly typical number of 10572 nodes and 28622 links. Also fairly typical, the major attributes on these links are type, length, speed, and capacity.

As pointed out above, this is enough information for the queue simulation. However, since the TRANSIMS micro-simulation is extremely realistic with respect to details such as number of lanes, turn and merge lanes, lane connectivity across intersections, or traffic signal phases, plausible defaults need to be generated for those elements from the available network files. For example, all intersections are assumed as ``no control'', which is a TRANSIMS category meaning that the simulation does not make any special provisions in order to deal with traffic stream priorities. The result will depend on the sequence in which the simulation goes through the links. More details can be found in [14].

The ``Gotthard'' Scenario

In order to test our set-up, we generated a set of 50000 trips going to the same destination. Having all trips going to the same destination allows us to check the plausibility of the feedback since all traffic jams on all used routes to the destination should dissolve in parallel. In this scenario, we simulate the traffic resulting from 50000 vehicles which start between 6am and 7am all over Switzerland and which all go to Lugano, which is in the Ticino, the Italian-speaking part of Switzerland south of the Alps. In order for the vehicles to get there, most of them have to cross the Alps. There are however not many ways to do this, resulting in traffic jams, most notably in the corridor leading towards the Gotthard pass. This scenario has some resemblance with real-world vacation traffic in Switzerland.

The ``Switzerland'' Scenario

For a realistic simulation of all of Switzerland, the starting point for demand generation is a 24-hour origin-destination matrix from the Swiss regional planning authority (Bundesamt für Raumentwicklung). For this matrix, the region is divided into 3066 zones. Each matrix entry describes the number of trips from one zone to another during a typical 24-hour workday; trips within zones are not included in the data. The original 24-hour matrix was converted into 24 one-hourly matrices using a three step heuristic which uses departure time probabilities and field data volume counts. These matrices are then converted to individual (disaggregated) trips using another heuristic. The final result is that for each entry in the origin-destination matrix we have a trip which starts in the given time slice, with origin and destination links in the correct geographical area. More details can be found in [14].

In the long run, it is intended to move to activity-based demand generation. Then, as explained above one would start from a synthetic population, and for each population member, one would generate the chain of activities for the whole 24-hour period.

Some Results

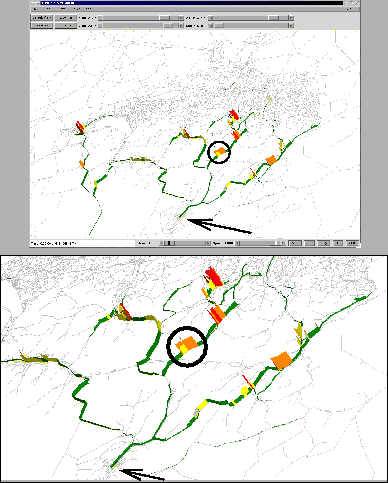
Figure 2 shows a typical result after 50 iterations with the TRANSIMS micro-simulation for the Gotthard scenario. The figures show the 15-minute aggregated density of the links in the simulated road network, which is calculated for a given link by dividing the number of vehicles seen on that link in a 15-minute time interval by the length of the link (in meters) and the number of traffic lanes the link contains. In all of the figures, the network is drawn as the set of small, connected line segments, re-creating the roadways as might be seen from an aerial or satellite view of the country. The lane-wise density values are plotted for each link as a 3-dimensional box super-imposed on the 2-dimensional network, with the base of a box lying on top of its corresponding link in the network, and the height above the ``ground'' set relative to the value of the density. Thus, larger density values are drawn as taller boxes, and smaller values with shorter boxes. Longer links naturally have longer boxes than shorter links. Also, the boxes are color coded, with smaller values tending toward green, middle values tending toward yellow, and larger values tending toward red. In short, the higher the density (the taller/redder the boxes), the more vehicles there were on the link during the 15-minute time period being illustrated. Higher densities imply higher vehicular flow, up to a certain point (the yellow boxes), but any boxes that are orange or red indicate a congested (jammed) link. All times given in the figures are at the end of the 15-minute measurement interval. The Gotthard tunnel is indicated by a circle; the destination in Lugano is indicated by an arrow.

As expected, many routes towards the single destination are equally used. In particular, many longer but uncongested routes are used in the final iteration (shown here) which are initially empty. It turns however out that only a subset of routes towards the final destination is used. This is related to the unrealistic intersection dynamics caused by the ``no control'' intersections: There are many plausible routes which are at a disadvantage at critical intersections and which are for that reason only used by very few vehicles.

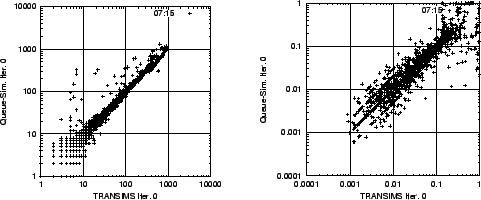
Figure 3 shows a snapshot of the initial run (i.e. without feedback) for the TRANSIMS micro-simulation and for the queue micro-simulation, both based on the same set of route plans. The visual similarity of both simulations is confirmed by analysis: Fig. 4 shows a link-by-link comparison between the two simulations for the time from 7am to 7:15am. It is clear that the two simulations are highly correlated in both quantities.

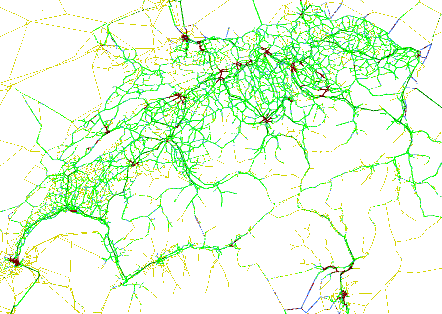
Figure 5 shows a preliminary result of the Switzerland scenario. In particular, this is a result before any feedback iterations were done. As one would expect, there is more traffic near the cities than in the country.

Abbildung 2: Snapshot at 8:00AM. The circle shows the traffic jam before the Gotthard tunnel. The arrow indicates the destination of all vehicles. TOP: All of Switzerland; BOTTOM: Zoom-In on interesting area

Abbildung 3: Iteration 0, 7h15; TOP: TRANSIMS; BOTTOM: Queue-Sim.

Abbildung 4: Link-by-link comparison TRANSIMS vs. Queue-Sim (iteration 0; 7h15). LEFT: Throughput. RIGHT: Density. The strong diagonal lines in the density comparison stem from links with very few cars on them: In those cases, they have very low densities which are related by small integer ratios, translating into constant offset on the logarithmic scales.

Abbildung 5: Switzerland at 8AM: Red (very dark gray) areas represent jammed traffic (in the cities); green and blue (mid-grays) represent flowing traffic; yellow (light gray) represents empty or nearly-empty roads. Very preliminary result.

Computational Issues

A metropolitan region can consist of 10 million or more inhabitants which causes considerable demands on computational performance. This is made worse by the relaxation iterations. And in contrast to simulations in the natural sciences, traffic particles ($=$ travelers, vehicles) have internal intelligence. As pointed out in the introduction, this internal intelligence translates into rule-based code, which does not vectorize but runs well on modern workstation architectures. This makes traffic simulations ideally suited for clusters of PCs, also called Beowulf clusters. We use domain decomposition, that is, each CPU obtains a patch of the geographical region. Information and vehicles between the patches are exchanged via message passing using MPI (Message Passing Interface).

Table 1 shows computing speeds for different numbers of CPUs for the queue simulation. The simulation scales fairly well for this scenario size and this computing architecture up to about 10 CPUs. The TRANSIMS micro-simulation is somewhat slower, but scales up to a RTR of 50 using about 30 CPUs [15,16]. In fact, the bottleneck to faster computing speeds is the latency of the Ethernet interface [15,16], which is about 0.5-1 msec. Since we have in the average six neighbors per domain meaning six message sends per time step, running 100 times faster than real time means that between 30% and 60% of the computing time is used up by message passing. As usual, one could run larger scenarios at the same computational speed when using more CPUs. However, running the same scenarios faster by adding more CPUs would demand a low latency communication network, such as Myrinet, or a supercomputer. Systematic computational speed predictions for different types of computer architectures can be found in Refs. [15,16].

Tabelle 1: Computational performance of the queue micro-simulation on a Beowulf Pentium cluster. The center column gives the number of seconds taken to run the first 3 hours of the Gotthard scenario. The right column gives the real time ratio (RTR), which is how much faster than reality the simulation is. A RTR of 100 means that one simulates 100 seconds of the traffic scenario in one second of wall clock time.

Number of Procs	Time elapsed	real time ratio
1	597	18.09
4	358	30.17
5	261	41.23
8	151	71.14
9	131	82.34
12	123	87.15
17	105	102.27
25	103	104.10
33	115	93.13

Summary

In terms of travelers and trips, a simulation of all of Switzerland, with more than 10 million trips, is comparable with a simulation of a large metropolitan area, such as London or Los Angeles. It is also comparable in size to a molecular dynamics simulation, except that travelers have considerably more ``internal intelligence'' than molecules, leading to complicated rule-based instead of relatively simple equation-based code. Such multi-agent simulations do not vectorize but run well on distributed workstations, meaning that the computing capabilities for such simulations have virtually exploded over the last decade.

This paper describes the status of ongoing work of an implementation of all of Switzerland in such a simulation. The whole simulation package consists of many modules, including the micro-simulation itself, the route planner, and the feedback supervisor which models day-to-day learning. The results of two micro-simulations are compared in order to check for errors in the simulation logic; a single destination scenario is used to verify the plausibility of the replanning set-up. Finally, a very preliminary result of a simulation of all of Switzerland is shown. Although considerable progress has already been made, much work is still to be done.

Acknowledgments

We thank the Swiss regional planning authority (Bundesamt für Raumentwicklung) for the input data.

Literatur

1

Vrtic, M.:
Dynamische Umlegung des Strassenverkehrs.
IVT Seminar, ETH Zürich, Dec 2001.
See www.ivt.baug.ethz.ch/vortraege

2

Beckman, R.J., Baggerly, K.A., McKay, M.D.:
Creating synthetic base-line populations.
Transportation Research Part A - Policy and Practice 30 (1996) 415-429

3

Vaughn, K., Speckman, P., Pas, E.:
Generating household activity-travel patterns (HATPs) for synthetic populations (1997)

4

Bowman, J.L.:
The day activity schedule approach to travel demand analysis.
PhD thesis, Massachusetts Institute of Technology, Boston, MA (1998)

5

Jacob, R.R., Marathe, M.V., Nagel, K.:
A computational study of routing algorithms for realistic transportation networks.
ACM Journal of Experimental Algorithms 4 (1999)

6

Nagel, K., Stretz, P., Pieck, M., Leckey, S., Donnelly, R., Barrett, C.L.:
TRANSIMS traffic flow characteristics.
Los Alamos Unclassified Report (LA-UR) 97-3530 (1997)

7

:
DYNAMIT/MITSIM (1999) Massachusetts Institute of Technology, Cambridge, Massachusetts. See its.mit.edu.

8

Barrett, C.L., Jacob, R., Marathe, M.V.:
Formal language constrained path problems.
Los Alamos Unclassified Report (LA-UR) 98-1739, see transims.tsasa.lanl.gov (1997)

9

TRANSIMS, TRansportation ANalysis and SIMulation System:
(since 1992) See transims.tsasa.lanl.gov.

10

Nagel, K., Schreckenberg, M.:
A cellular automaton model for freeway traffic.
Journal de Physique I France 2 (1992) 2221

11

Gawron, C.:
An iterative algorithm to determine the dynamic user equilibrium in a traffic simulation model.
International Journal of Modern Physics C 9 (1998) 393-407

12

Simon, P.M., Nagel, K.:
Simple queueing model applied to the city of Portland.
International Journal of Modern Physics C 10 (1999) 941-960

13

Rickert, M.:
Traffic simulation on distributed memory computers.
PhD thesis, University of Cologne, Germany (1998) See www.zpr.uni-koeln.de/~mr/dissertation.

14

Voellmy, A., Vrtic, M., Raney, B., Axhausen, K., Nagel, K.:
Status of a TRANSIMS implementation for Switzerland (in preparation)

15

Rickert, M., Nagel, K.:
Dynamic traffic assignment on parallel computers in TRANSIMS.
Future generation computer systems 17 (2001) 637-648

16

Nagel, K., Rickert, M.:
Parallel implementation of the TRANSIMS micro-simulation.
Parallel Computing (in press)

Über dieses Dokument ...

Towards a Microscopic Traffic Simulation of All of Switzerland

This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)

Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department, Macquarie University, Sydney.

The command line arguments were:
latex2html -split 1 -dir html cse-adam-02.tex

The translation was initiated by Kai Nagel on 2002-05-07