


Nächste Seite: Über dieses Dokument ...
documentclass[a4paper,10pt,oneside,onecolumn,titlepage,final]article
usepackage[a4paper,left=1.25in,right=1.25in,top=1in,bottom=1in]geometry
usepackagetimes
usepackagehelvet
usepackagetabularx
usepackagefancyhdr
makeatletter
letKEEPheadruleheadrule
letheadruleundefined
letKEEPfootrulefootrule
letfootruleundefined
makeatother
usepackagegraphicx
usepackageamssymb
usepackage[nooneline]caption
par
usepackagetitlesec
titleformatsectionLargesffamilybfseriesthesection.1em
titleformatsubsectionlargesffamilybfseriesthesubsection1em
titleformatsubsubsectionnormalfontsffamilybfseriesthesubsubsection1em
par
titleformatparagraph[hang]normalfontsffamilybfseriesitshape0pt
par
titleformatsubparagraph[hang]smallsffamilybfseriesitshape0pt
par
usepackagenatbib
par
usepackagegerman
selectlanguageUSenglish
par
letheadruleKEEPheadrule
letfootruleKEEPfootrule
par
pagestylefancy
lheadtextitInternational Conference on Travel Behaviour Research
rheadtextitAugust 10-14, 2003
par
setlengthparindent0in
setlengthparskip10pt
par
newedcommandmytitleAgent-Based Activities Planning for an Iterative Traffic Simulation of Switzerland
par
usepackagesubfigure
par
begindocument
par
begintitlepage
par
hrule
begincenter
includegraphics[width=0.5hsize]plans-server-design-gz.eps
endcenter
hrule
par
sffamily
par
vspace0.5in centerLARGEtextbfmytitle
par
vspace0.5in Large
noindent textbfBryan Raney, Institute for Computational Science, ETH Zürich
noindent textbfMichael Balmer, Institute for Computational Science, ETH Zürich
noindent textbfKay Axhausen, Institute for Transport Planning and Systems (IVT), ETH Zürich
noindent textbfKai Nagel, Institute for Computational Science, ETH Zürich
par
par
vspace0.25in noindent textbflarge Conference paper
textbflarge Session XXX
par
sffamily
vspace0.25in
par
begintabular[b]cp5in
par
includegraphics[width=1.15in]iatbr_logo.eps.gzhspace0.1in& large
vspace-0.75in
textbfMoving through nets:newline
textbfThe physical and social dimensions of travelnewline
10
International Conference on Travel Behaviour Researchnewline
Lucerne, 10-14. August 2003
par
endtabular
par
par
vfilleject
par
setcounterpage1
par
vspace0.25in noindent textbfsffamilyLarge mytitle
par
noindent Bryan Raney
Institute for Computational Science
ETH Zürich
CH-8092 Zürich, Switzerland
par
noindent parbox[t]0.5inPhone: +41 (0)1 632 08 92
parbox[t]0.5inFax: +41 (0)1 632 13 74
parbox[t]0.5ineMail: braney@inf.ethz.ch
par
noindent Michael Balmer
Institute for Computational Science
ETH Zürich
CH-8092 Zürich, Switzerland
par
noindent parbox[t]0.5inPhone: +41 (0)1 632 03 64
parbox[t]0.5inFax: +41 (0)1 632 13 74
parbox[t]0.5ineMail: balmermi@inf.ethz.ch
par
noindent Kay Axhausen
Institute for Transport Planning and Systems (IVT)
ETH Hönggerberg
CH-8093 Zürich, Switzerland
par
noindent parbox[t]0.5inPhone: +41 (0)1 633 39 43
parbox[t]0.5inFax: +41 (0)1 633 10 57
parbox[t]0.5ineMail: axhausen@ivt.baug.ethz.ch
par
noindent Kai Nagel
Institute for Computational Science
ETH Zürich
CH-8092 Zürich, Switzerland
par
noindent parbox[t]0.5inPhone: +41 (0)1 632 27 54
parbox[t]0.5inFax: +41 (0)1 632 13 74
parbox[t]0.5ineMail: nagel@inf.ethz.ch
par
vspace0.25in noindent textbfsffamilyLarge Abstract
par
noindent In a multi-agent transportation simulation, travelers are represented
as individual ``agents'' who make independent decisions about their
actions. We are implementing a large-scale version of such a
simulation in order to model the traveler behavior in all of
Switzerland.
par
Our simulation is composed of separate modules. Each module models a
different set of decisions made by an agent, and calculates those
decisions independently for each agent. The modules we use are listed
below.
par
The textbfactivities generator module generates a complete 24-hour
day-plan for a given agent, including each major activity (sleep, eat,
work, shop, drink beer) the agent wishes to accomplish during the day,
their times, and their locations. Activity times may be flexible, and
can be specified by some combination of starting time, duration,
and/or ending time.
par
The textbfroute planner module determines the mode of
transportation, as well as the actual route plan taken, for each leg
of the agent's chosen activity plan. Each leg simply connects one
activity to another. At present our router generates routes only for
automobile travel.
par
The textbfmicro-simulation module executes all the agents' plans
simultaneously and in consequence computes the interaction between
different travelers, leading e.g. to congestion. The micro-simulation
provides data to the other modules about what happened during the
simulated day, including the travel-time information described above,
as well as the time and location of significant events to happen to
agents while they are being simulated (such as arriving at their first
activity destination, etc.).
par
There is an interdependence between the above modules. For example,
plans depend on congestion (via travel-times) but congestion is a
result of the execution of plans. The textbffeedback and learning
module resolves the interdependence via an iterative method, where an
initial plans set is slowly adapted until it is consistent with the
resulting travel conditions, or until some other stopping criterion is
fulfilled.
In this technique, each iteration of the simulation can been seen as a
separate ``day'' in the life of the agents. Each day the agents' view
of the traffic network is updated, and they learn about which plans
work well and which do not.
par
We implement the feedback mechanism with a so-called textbfagent
database that allows agents to have a ``memory'' of the plans they
have used during past days in the current iteration sequence. The
agents also use the events data from the micro-simulation to determine
performance ``scores'' for each plan. Each day of the iteration,
every agent chooses a plan from its memory based on their scores, or
decides to generate a brand-new plan (either a new set of route plans
for a given activity-set or a new activity-set and associated route
plans) based on information from the past.
par
This paper goes beyond what we have done in the past by investigating
for the first time the effects of time choice inside the feedback
loop. That is, travel time results are fed back to the time selection
module, which reacts by constructing time schedules that avoid, for
example, congestion.
This paper contains preliminary verification results; a real-world
case study is planned soon.
par
vfill
par
vspace0.25in noindent textbfsffamilyLarge Keywords
par
noindent Traffic Simulation, Transportation Planning, Route Planning, Activities Planning, International Conference on Travel Behaviour Research, IATBR
par
vspace0.25in noindent textbfsffamilyLarge Suggested citation
par
noindent
Raney, Bryan, Michael Balmer, Kay Axhausen, and Kai Nagel (2003) mytitle, paper
presented at the 10th International Conference on Travel Behaviour
Research, Lucerne, August 2003.
par
endtitlepage
par
yy TODO: Make a high-resolution (300 ppi) digital file for each image, in JPEG or TIFF file.
par
sectionIntroduction
par
There is widespread agreement that, at least from a theoretical
perspective, the traditional 4-step process has reached its limits.
Demand generation in the traditional 4-step process is decoupled both
from time-of-day and from demographics. This means that important
sensitivities and effects, such as peak spreading, time-dependent tolls,
or income-dependent behavior, cannot be modeled.
par
It is possible to include both of these aspects via the widely
discussed activity-based demand generation. However, the
representation of traffic in the 4-step process in independent from
time. It is difficult to see how a time-dependent demand structure
can be mapped on a time-independent traffic system and how results for
time-dependent questions can still be meaningful.
par
In consequence, there are many attempts to make traffic assignment
dynamic. This starts with incremental changes to the static
assignment citep[e.g.][]Kaufman:etc:91,VISUM:dynamic,METROPOLIS.
yy metropolis paper is published, should have complete reference
However, all of these approaches need to sacrifice the nice uniqueness
feature of static assignment, and it is unlikely that something
similarly nice exists at all citepDaganzo:assign-w-queues. This
indicates that, once one has to give up time-independence, then a
completely new start might be a better option. Such new starts,
called Dynamic Traffic Assignment (DTA) and being entirely
simulation-based, have been pursued by a considerable number of
groups. At this point, one can maybe, despite many overlaps,
distinguish the following different directions:
beginitemize
par
item Some groups are driven by requirements from the Intelligent
Transportation Systems (ITS) initiatives. The ITS technology of
adaptive route guidance demands that models are time-dependent, and
that they can model time-dependent reactions of drivers (e.g. DYNASMART citepDYNASMART, DYNAMIT citepDYNAMIT).
par
item Some groups have an interest in a rather complete representation
of the complete traffic dynamics while still having acceptable
computing speeds. This is in general achieved by using advanced
parallel computing concepts citep[e.g.][]TRANSIMS.
par
item Some other groups have instead concentrated on using a rather
minimal representation of the traffic dynamics. The advantages of
this are larger computational speed, and better conceptual clarity
citep[e.g.][]Gawron:queue,ch.
par
item Finally, there are attempts to understand the theoretical
aspects of this new approach
citep[e.g.][]Cascetta:Cantarella:day2day,Bottom:thesis,Watling:stochastic,Bliemer:personal.
par
yy replace bliemer:personal by better reference in later versions
par
enditemize
par
Now once traffic assignment is dynamic, it is conceptually
straightforward to couple it to time-dependent demand. For historical
reasons, however, at this point the method to couple time-dependent
demand generation and time-dependent traffic assignment is via
time-dependent origin-destination (OD) matrices. That is, the system
generates for each time slice, say for each hour, the typical matrix
of trips going from each zone to each other zone. The traffic
assignment reads all these matrices, and computes the resulting
equilibrium routes.
par
When thinking about this, it is quickly clear that this method is
giving up some of the potential advantages of the activity-based
approach. For example, delays along the time axis (delays in the
morning will cause delays in the evening) are completely lost in the
OD-matrix approach since activity chains are decomposed into trips
which are treated completely independent. Also, using the OD matrix
once more decouples the route assignment completely from any
demographic information that may be there.
par
A possible alternative is to maintain the identity of the traveler
throughout the system. That is, instead of having the demand
generation write OD matrices, it could write individual activity
chains for each traveler, which the route assignment part of the code
would then read and then via DTA find routes for those activity
chains. One could even go further and include the activity generation
into the feedback process (adapting activity time, activity location,
or even activity participation to the delay structure in the
transportation system).
par
The maybe only operational approach at that level is TRANSIMS
citepTRANSIMS. The TRANSIMS is essentially finished and has been
run on a Portland case study, but despite much documentation, we are
unable to find results of this study with respect to real world
behavior citepTRANSIMS:Portland.
par
The approach of TRANSIMS would now probably be called ``agent-based''
or ``multi-agent'', since it tracks each individual traveler agent
through its day. The TRANSIMS design, however, is somewhat contrary
to an agent-based design, since it does not keep consolidated person
information in one place, but has, say, demographic data, activity
plans, route plans, performance information, or information about past
plans all in different files. Nevertheless, the agent-based
information can be reconstructed if needed.
par
Our own research has been oriented to extend TRANSIMS to make it
entirely agent-based (which means to have consolidated agent
information, and also to actually use it, for example by explicitly
using several plans per agent), and then to move away from the
day-to-day logic that is inherently included in the existing TRANSIMS
design. This paper is an intermediate result along the way to that
eventual goal. We have already in the past achieved a completely
agent-based dynamic traffic assignment citepch. The behavior of
that system was similar to other existing DTA systems, but it had the
following differences:
beginitemize
par
item The traffic microsimulation was, because of parallel computing
technique, considerably faster than any other approach we are aware of
- it is capable to compute a complete car traffic of a 24-hour day
for a population of several millions in several minutes
citepqueue.
par
item The whole approach was, via an agent database, completely
agent-based. That is, each agent ``remembers'' all plans that it ever
executes during the simulation process, together with scores that
measure the performance of each plan. In general, the agent selects
between the ``known'' plans with a multinomial logit model, but from
time to time, a random plan is tested or new plans are added.
par
enditemize
par
This paper now goes beyond DTA and for the first time includes
activity feedback into the process. Although in the long run it is
intended to include the complete activity planning process, consisting
of activity pattern choice, activity location choice, and activity
time choice, into the process, at this point only a time choice module
was available. This paper in consequence refers to activity time
choice only; for information regarding other dimensions of activity
replanning, please see citepga4acts.
par
Time choice for whole activities means that we assume activities plus
their locations are given, but the traveler-agent still needs to decide
how much time to allocate to each activity, and when to start the
whole chain. This problem is related to departure time choice
citep[e.g.][]Arnott:etc:bottleneck,METROPOLIS, but it is more
complicated: The task is to position the whole activity chain
optimally into the complete day. This means that, in contrast to
conventional departure time modeling, a traveler that has a lot of
activities planned after work is more apt to start early than one
without this. In addition, the system picks up travel time
information at the time choice level. That is, it will include
knowledge about travel times from one activity to the next, as a
function of time-of-day, into the decision-making process.
par
This paper will be structured as follows: After an explanation of the
overall simulation structure (Sec. refsec:structure), where all the
different modules are explained, it will discuss the utility function
that is used for scoring different plans (Sec. refsec:util-fcns).
This is then followed by a section discussing results which are
obtained with a testing scenario, which is used to establish the
functionality of the code (Sec. refsec:test-case). Sec. refsec:discussion
will discuss some of the artifacts of our preliminary results,
from which assumptions they derive, and how we intend to improve the
system. This section will also contain some outlook on our future
plans regarding real-world activity-based simulations. The paper is
concluded by a summary.
par
sectionSimulation Structure
labelsec:structure
par
Traffic simulations for transportation planning typically consist of
the following modules (Fig. reffig:bubbles):beginitemize
par
item textbfPopulation generation. Demographic data is
disaggregated so that one obtains individual households and
individual household members, with certain characteristics, such
as a street address, car ownership, or household
income citepBeckman:pops. - This module is not used for our
current investigations but will be used in future.
par
item textbfActivities generation. For each individual, a set of
activities (home, going shopping, going to work, etc.) and activity
locations for a day is
generated citepVaughn:etc:HATPs,Bowman:thesis. - This module is
introduced in this paper.
par
item textbfModal and route choice. For each individual, the
modes are selected and routes are generated that connect activities
at different locations (see Sec. refsec:router). The routing
should be dynamic in order to adequately model time-dependent
congestion effects.
par
item textbfMobility simulation. Up to here, all individuals have
made emphplans (or emphstrategies) about their behavior. The
mobility simulation executes all those plans simultaneously (see
Sec. refsec:mobsim). In particular, we now obtain the result of
emphinteractions between the plans - for example congestion.
par
item textbfFeedback. In addition, such an approach needs to make
the modules consistent with each other (Sec. refsec:learning).
For example, plans depend on congestion, but congestion depends on
plans. A widely accepted method to resolve this is systematic
relaxation citepKaufman:etc:91,Nagel:thesis,Bottom:thesis - that
is, make preliminary plans, run the traffic micro-simulation, adapt
the plans, run the traffic micro-simulation again, etc., until
consistency between modules is reached. The method is somewhat
similar to the Frank-Wolfe-algorithm in static assignment, or in
more general terms to a standard relaxation technique in numerical
analysis.
par
enditemize
This modularization has in fact been used for a long time; the main
difference to earlier implementations is that it is now feasible to
make all modules completely microscopic, i.e. each traveler is
individually represented in all modules.
par
As of now, not all of the above modules are currently implemented.
This paper discusses results obtained with a version of the simulation
system that consists of car-only versions of the activity generator,
the router, the mobility simulation, and the feedback.
par
These modules will be described in more detail in the following
sub-sections. It should be noted that in particular the feedback
system is unique in that it explicitly keeps track of many strategies
of each individual traveler. Most simulation systems assume either
only one strategy per traveler, or they group travelers together
according to their characteristics, for example by common destination.
par
beginfigure
begincenter
captionSimulation modules.
labelfig:bubbles
vspace1em
hrule
vspace1em
includegraphics[width=0.7hsize]transims-bubbles-fig.eps
endcenter
hrule
endfigure
par
subsectionThe Day Plan with Activities
par
The activities generator (Sec. refsec:acts-gen) and router
(Sec. refsec:router) modules are used by the agents in the
simulation system to make decisions and fill in parts of their plan
(or emphstrategy) for each day.
par
That plan is a list of activities to be executed throughout the entire
day (24 hours), and the trips connecting the activities. Activities
describe what the agent wants to do or where it wants to be during the
day, and trips describe how the agent moves from one activity to the
next. Trips are handled by the router, described in
Sec. refsec:router.
par
Each activity in the day's plan is described by a type (e.g. home,
work, shopping, leisure), a location, and timing information. Timing
information usually consists of just the activity's duration, but
might also include an absolute ending time (i.e. closing time for
shops).
par
note three parts to activities feedback
par
The process an agent can use to generate an activity plan can be
divided into three parts: pattern choice, location choice, and timing
choice.
par
The emphpattern choice determines which activities to perform
during the day, and in what order. For example, and agent might
decide whether or not to go shopping, and if so, before or after work.
par
The emphlocation choice determines where the agent will perform
each activity. For some activities, such as home/sleeping, and work,
this decision is made very infrequently, while for other activities,
such as shopping, the agent might choose a different location each
time it wants to perform the activity. (E.g., bakery close to home,
grocery store near work)
par
The emphtime choice determines the specific timing of when to start
the day, and how much time to allocate to each activity.
par
These decisions can be made all at once by a single module, or
separate modules can be used to handle each one individually. For
this paper we have only implemented the time choice decision module,
and keep the activity pattern and locations fixed. This module is
described in the next section.
par
subsectionActivities Generation Module
labelsec:acts-gen
par
Given the current traffic situation and an activity pattern with
specified locations, the activities generation module calculates the
optimal durations to apply to each activity.
par
note Connections
par
The activities generator is aware of the traffic situation because it
reads the events information provided by the mobility simulation (see
Sec. refsec:mobsim). From this information it builds a
representation of the travel times that were encountered by agents
traveling from one location in the network to another starting at
various times of day. The data is stored by geographic coordinates
and by time of day, which for speed is aggregated into 15-minute time
bins. From this model the module can estimate the time it would take
to make any arbitrary trip within the network by matching nearby
coordinates and/or travel-times and interpolating the desired data
from them.
par
note GA
par
This module uses a genetic algorithm approach to generate plans. Each
activity type (work, shop, etc.) has a specific emphutility
function that tells the module how much ``good'' an activity does for
its agent. The specific utility functions are described below in
Sec. refsec:util-fcns. The utility of an activity is determined by
comparing the specific time of day that the agent starts performing
that activity, the time when the agent stops, and how long the agent
on that activity spent in total with the activities ``preferred''
start time, end time and duration.
par
The genetic algorithm essentially compares the utilities of many
different potential plans and chooses the best one. A potential plan
is just a proposed set of durations for the activities. The first
activity in the plan (typically ``home'') always begins at midnight
(00:00) and the last activity (also ``home'') ends at midnight
(24:00). Coupling this information with the proposed durations and
the estimates of the trip times from the connection data, the module
can compute a score for any potential plan.
par
The genetic algorithm searches for an optimal (or near-optimal) plan
using the standard operations of genetic algorithms, mutation and
crossover. Mutation causes a random alteration of a plan, while
crossover combines the information from two plans into a new plan.
For reasons of speed this process is cut off after 250 ``generations''
of plans (using a population size of 25), and the best plan is
returned to the agent.
par
One important consequence is that the algorithm returns only one
solution. That solution is the best one that the GA has found within
the time allocated to it. This is in stark difference to standard
random utility models that chose between different options with
exponentially weighted probabilities. As one will see later, this
causes many travelers to concentrate on the same options, rather than
spreading out through time.
par
yy above may need modif once rnd seed is changed every time when time
ch module is called
par
subsectionRouting Module
labelsec:router
par
Successive activities at different locations are connected by trips
that use the transportation network. Trips are described by their
mode and mode-specific information. For example, a car-mode trip
contains a description of the vehicle's route through the network from
the location of the previous activity to the location of the next
activity. In principle trips can be selected from different mode
types, but at present we only model car trips.
par
The routing module generates those paths that guide agents through the
network, as part of the description for the trips that connect their
activities. The trips have (expected) starting times, and the router
needs to be sensitive to congestion so that it tends to avoid
congested links.
par
The router we use for the present study is based on Dijkstra's
shortest-path algorithm, but ``shortness'' is measured by the time it
takes an agent to travel down a link (road segment) in the network.
These times depend on how congested the links are, and so they change
throughout the day. This is implemented in the following way: The way
a Dijkstra algorithm searches a shortest path can be interpreted as
expanding, from the starting point of the trip, a network-oriented
version of a wave front. In order to make the algorithm
time-dependent, the speed of this wave front along a link is made to
depend on when this wave front enters the link citep[e.g.][]Jacob:etc:comp.
par
That is, for each link 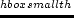 we need a function
we need a function  which returns
the link ``cost'' (
which returns
the link ``cost'' (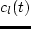 link travel time) for a vehicle entering at
time
link travel time) for a vehicle entering at
time  . This information is taken from a run of the traffic
simulation. In order to make the look-up of
. This information is taken from a run of the traffic
simulation. In order to make the look-up of 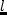 reasonably fast,
we aggregate over 15-min bins, during which the cost function is kept
constant. That is, all vehicles entering a link between e.g. 9am and
9:15am will contribute to the average link travel time during that
time period.
par
subsectionMobility Simulation
labelsec:mobsim
par
As a traffic micro-simulation we use an improved version of a
so-called ``queue simulation'' citepGawron:queue. The improvements
are an implementation on parallel computers, and an improved
intersection dynamics, which ensures a fair sharing of the
intersection capacity among incoming traffic
streams citepqueue,queue-trb03. The details of the traffic simulation
are not particularly important for this paper; we expect many traffic
simulations to reproduce similar results. The important features of
our simulation are:beginitemize
par
item Plans following. The feedback framework generates individual
day plans for each individual vehicle, and the traffic simulation
needs to have travelers/vehicles which follow those plans.
This implies that the traffic simulation needs to be microscopic,
that is, all individual travelers/vehicles are resolved. Beyond
that, however, it does not prescribe the dynamics; everything is
possible from smooth particle hydrodynamics (e.g. DYNAMIT,
DYNASMART) to virtual reality micro-simulations (e.g. TRANSIMS).
par
item Trip chaining. As described in Sec. refsec:acts-gen, the day plan
of an agent consists of a list of activities (with associated
durations) and the trips needed to connect the activities. The
trips are not independent, but ``chained'' together throughout the
day. The simulation should be implemented so that a late arrival
(due to traffic congestion) of one trip shifts the rest of the day's
schedule accordingly.
par
item Computational speed. We need to run many simulations of
24-hour days -- usually about 50 emphfor a single scenario.
This means that a computational speed of 100 times faster than real
time on a road network with several thousands of links (road
segments) and several millions of travelers is desirable. Our queue
simulation demonstrates that this is feasible.
par
item Congestion build-up and queue spillback. Although this is not a
requirement for the framework in general, the results of the present
paper depend on the fact that congestion normally starts at
bottlenecks (i.e. where demand is higher than capacity), but then
spills backwards into the system and across intersections. Once
such congestion is there, it takes a long time to dissolve.
The model should
reflect this, emphand it should reflect the physical space that
the queued vehicles occupy in the system.
enditemize
par
We keep the simulation as simple as we can, which means we do not
perform any data aggregation within the simulation. It simply dumps
out raw data, in the form of ``events,'' which tell the time and
location where something interesting happens to an agent. These
events can be parsed and aggregated, if necessary, by the other
modules to obtain any information they may need about what happened in
the simulation. At present the simulation only outputs events for
agents entering or exiting a link, but other interesting events might
be when agents encounter congestion, change speed, etc.
par
A major advantage of the queue simulation, besides its simplicity, is
that it can run directly off the data typically available for
transportation planning purposes. This is no longer true for more
realistic simulations, which need, for example, the number of
lanes including pocket and weaving lanes, turn connectivities across
intersections, or signal schedules.
par
subsectionLearning and Feedback via the Agent Database
labelsec:learning
par
As mentioned above, plans (such as routes) and congestion need to be
made consistent. This is achieved via a relaxation technique
citepKaufman:etc:91,Nagel:thesis,Bottom:thesis:
beginenumerate
par
item The system begins with an initial set of strategies, one per
agent. The initial strategy is the fully specified activity plan
connected by trips with routes based on free speed travel times,
which represent a network with no congestion.
par
item For each agent, the new strategy is stored in the
agent database citepRaney:Nagel:strc2002,agdb, which represents
its memory of previously tried strategies. Since the agents have
only one strategy apiece, they automatically select this as their
next strategy to execute.
par
item labelit:sim The traffic simulation is executed with the set
of selected strategies.
par
item Each agent measures the performance of its strategy based on
the outcome of the simulation. ``Performance'' is measured by the
same utility functions as used by the activities generator,
described in Sec. refsec:util-fcns. This information is stored
for all the agents in the agent database, associated with the
strategy that was used.
par
item labelit:frac If less than 100 iterations have been performed so
far in the cycle, then 20% of the population chooses to obtain a
new plan they have never tried before. (After 100 iterations, plans
are only chosen from memory.) Each agent picks a strategy at random
from its memory and sends it to either the activities generator or
route planner (with equal probability) to update it based on the
newest travel-time data from the last traffic simulation. The
returned plan is added to the agent database as a new strategy and,
being new, is mandatorialy selected by the agent for the next
simulation run. Note that plans coming from the activities generator
are also sent to the router for updated routes.
par
Since the router needs trip start times to create a route, these are
estimated from the durations of the activities preceding the trip,
and from the travel times most recently encountered by an agent for
the trips preceding the current trip. Durations are always known,
but if travel-time for a trip is missing, it is assumed to be 0.
par
item labelit:select 70% of the agents (or 90% if past iteration
100) choose a previously tried strategy from the agent database, by
comparing the performance values for the different strategies,
without looking at any other information about them. Specifically,
they use a multinomial logit model citepBen-Akiva:book
reasonably fast,
we aggregate over 15-min bins, during which the cost function is kept
constant. That is, all vehicles entering a link between e.g. 9am and
9:15am will contribute to the average link travel time during that
time period.
par
subsectionMobility Simulation
labelsec:mobsim
par
As a traffic micro-simulation we use an improved version of a
so-called ``queue simulation'' citepGawron:queue. The improvements
are an implementation on parallel computers, and an improved
intersection dynamics, which ensures a fair sharing of the
intersection capacity among incoming traffic
streams citepqueue,queue-trb03. The details of the traffic simulation
are not particularly important for this paper; we expect many traffic
simulations to reproduce similar results. The important features of
our simulation are:beginitemize
par
item Plans following. The feedback framework generates individual
day plans for each individual vehicle, and the traffic simulation
needs to have travelers/vehicles which follow those plans.
This implies that the traffic simulation needs to be microscopic,
that is, all individual travelers/vehicles are resolved. Beyond
that, however, it does not prescribe the dynamics; everything is
possible from smooth particle hydrodynamics (e.g. DYNAMIT,
DYNASMART) to virtual reality micro-simulations (e.g. TRANSIMS).
par
item Trip chaining. As described in Sec. refsec:acts-gen, the day plan
of an agent consists of a list of activities (with associated
durations) and the trips needed to connect the activities. The
trips are not independent, but ``chained'' together throughout the
day. The simulation should be implemented so that a late arrival
(due to traffic congestion) of one trip shifts the rest of the day's
schedule accordingly.
par
item Computational speed. We need to run many simulations of
24-hour days -- usually about 50 emphfor a single scenario.
This means that a computational speed of 100 times faster than real
time on a road network with several thousands of links (road
segments) and several millions of travelers is desirable. Our queue
simulation demonstrates that this is feasible.
par
item Congestion build-up and queue spillback. Although this is not a
requirement for the framework in general, the results of the present
paper depend on the fact that congestion normally starts at
bottlenecks (i.e. where demand is higher than capacity), but then
spills backwards into the system and across intersections. Once
such congestion is there, it takes a long time to dissolve.
The model should
reflect this, emphand it should reflect the physical space that
the queued vehicles occupy in the system.
enditemize
par
We keep the simulation as simple as we can, which means we do not
perform any data aggregation within the simulation. It simply dumps
out raw data, in the form of ``events,'' which tell the time and
location where something interesting happens to an agent. These
events can be parsed and aggregated, if necessary, by the other
modules to obtain any information they may need about what happened in
the simulation. At present the simulation only outputs events for
agents entering or exiting a link, but other interesting events might
be when agents encounter congestion, change speed, etc.
par
A major advantage of the queue simulation, besides its simplicity, is
that it can run directly off the data typically available for
transportation planning purposes. This is no longer true for more
realistic simulations, which need, for example, the number of
lanes including pocket and weaving lanes, turn connectivities across
intersections, or signal schedules.
par
subsectionLearning and Feedback via the Agent Database
labelsec:learning
par
As mentioned above, plans (such as routes) and congestion need to be
made consistent. This is achieved via a relaxation technique
citepKaufman:etc:91,Nagel:thesis,Bottom:thesis:
beginenumerate
par
item The system begins with an initial set of strategies, one per
agent. The initial strategy is the fully specified activity plan
connected by trips with routes based on free speed travel times,
which represent a network with no congestion.
par
item For each agent, the new strategy is stored in the
agent database citepRaney:Nagel:strc2002,agdb, which represents
its memory of previously tried strategies. Since the agents have
only one strategy apiece, they automatically select this as their
next strategy to execute.
par
item labelit:sim The traffic simulation is executed with the set
of selected strategies.
par
item Each agent measures the performance of its strategy based on
the outcome of the simulation. ``Performance'' is measured by the
same utility functions as used by the activities generator,
described in Sec. refsec:util-fcns. This information is stored
for all the agents in the agent database, associated with the
strategy that was used.
par
item labelit:frac If less than 100 iterations have been performed so
far in the cycle, then 20% of the population chooses to obtain a
new plan they have never tried before. (After 100 iterations, plans
are only chosen from memory.) Each agent picks a strategy at random
from its memory and sends it to either the activities generator or
route planner (with equal probability) to update it based on the
newest travel-time data from the last traffic simulation. The
returned plan is added to the agent database as a new strategy and,
being new, is mandatorialy selected by the agent for the next
simulation run. Note that plans coming from the activities generator
are also sent to the router for updated routes.
par
Since the router needs trip start times to create a route, these are
estimated from the durations of the activities preceding the trip,
and from the travel times most recently encountered by an agent for
the trips preceding the current trip. Durations are always known,
but if travel-time for a trip is missing, it is assumed to be 0.
par
item labelit:select 70% of the agents (or 90% if past iteration
100) choose a previously tried strategy from the agent database, by
comparing the performance values for the different strategies,
without looking at any other information about them. Specifically,
they use a multinomial logit model citepBen-Akiva:book
for the probability 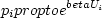 to select route
to select route 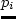 , where
, where 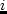 is
the corresponding memorized total utility and
is
the corresponding memorized total utility and 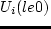 is an
empirical constant. This process is explained in detail
in citetRaney:Nagel:strc2002,fgcs,agdb. We differ from these by
setting
is an
empirical constant. This process is explained in detail
in citetRaney:Nagel:strc2002,fgcs,agdb. We differ from these by
setting 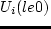 to 0.01 in this work.
par
item labelit:random The rest of the agents (10%) choose a plan
emphat random from their memory, using a uniform probability for
each plan, and ignoring plan performance.
The value of
to 0.01 in this work.
par
item labelit:random The rest of the agents (10%) choose a plan
emphat random from their memory, using a uniform probability for
each plan, and ignoring plan performance.
The value of 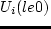 in step refit:select effects how likely
agents choose ``non-best'' plans. Higher values of
in step refit:select effects how likely
agents choose ``non-best'' plans. Higher values of 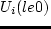 lead
toward the best plan being chosen more often, while smaller values
provide a more randomized choice.
This random choice ensures that no matter what the value of
lead
toward the best plan being chosen more often, while smaller values
provide a more randomized choice.
This random choice ensures that no matter what the value of 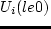 is, no plan is left out of consideration. Some agents will be sure
to use even the worst plans in their memory (which may or may not
improve their performance with successive tries).
par
item labelit:relax This cycle (i.e. steps refit:sim
through refit:select) is run for 150 times. Note that in the
last 50 cycles no new plans are created by the agents.
par
endenumerate
par
sectionUtility Functions for the Day Plan
labelsec:util-fcns
par
note Explain the problem
par
When the activities generator module generates the timing for the
activity schedule, it optimizes over the emphentire day all at
once, not piece-by-piece. This is to allow trade-offs between the
different parts of the day. For example, if the day has a large
number of activities that need to be accomplished, the activities
generator module should be able to do something like shorten the first
activity (i.e. leave home earlier) in order to fit the extra
activities at the end of the day. It should consider the travel-times
of the trips between the activities when scheduling them as well, so
as not to waste more time than necessary driving around. This might
mean temporally grouping activities that are geographically near one
another to avoid driving across town more times than necessary.
par
The module must solve a problem similar to, but not the same as,
departure time choice. One difference is that departure time choice
makes decisions for each trip independently from one another
citepMETROPOLIS, rather than allowing trade-offs between them.
Also, while the activity durations chosen by the activities generation
module directly effect the departure times of the agents' trips, those
departure times are not fixed. If, for example, an agent arrives late
to one activity, the agent will stay at the activity for the chosen
duration, rather than leaving early to stick to the departure time of
the next trip. In essence, priority is given to the timing of
activities over timing of trips, since the activities motivate the
trips, and not the other way around.
par
yy in a future version of this paper, this needs to be explained
better. we should explain what is the output of the time choice
module, and how the usim deals with it.
par
We were unable to find a single reference where we could look up a
meaningful set of utility functions to implement. As a result our
group has implemented two prototypes of activities generators with
their inclusive utility functions. The more ``diligent'' module of
the two, by D. Charypar, was not completed in time to use for this
study, but it will be presented at IATBR citepga4acts. Instead,
this work uses the simpler module by A. Schneider, which is described
here and elsewhere in this paper citepSchneider:act-times.
par
note Utility
par
In order for the activities generation module to calculate the optimal
day plan for an agent, it must have some way to evaluate the plan.
The utility function provides a way to do this by describing the
utility, or usefulness, the plan has to the agent (if the plan is not
useful, why would the agent execute it?). The utility function
translates the layout of the plan into a numerical value, which can be
thought of as a score or an actual value in monetary terms.
par
The utility of the day plan must incorporate the utilities for each
component of the plan. Those seperate utilities must be set relative
to one another so that they can be compared appropriately when making
trade-offs. In other words, changing a parameter of a more important
activity by a certain amount should effect the total utility more than
more than the same change on a less important activity.
par
Since location choice is currently not implemented, the different
activity types are differentiated only by their timing information.
In the utility function used for this paper, each activity type has a
preferred duration, and preferred time windows for when agents should
begin and end activities of that type. Different agents could have
different preferences for a given activity type, but in the current
implementation we give identical preferences to all agents.
par
Not all preferences of all activities in a day's plan can necessarily
be met, so the activity generator's job is to find the best compromise
between the specifications of each activity in order to make the whole
day as useful as possible to the agent.
par
The utility of the day plan measures the usefulness of that plan, or
how well it meets the needs of the agent. It is just the sum of the
utilities of each activity, plus the utilities of each trip. These
calculations are explained next.
par
subsectionUtility of a Single Activity
par
The utility function for a single activity measures how closely an
activity of a certain type (e.g. home or work) matches the preferences
set for that type.
par
An ``ideal'' instance of an activity would achieve the maximum
utility, which we set to 0.
As an activity instance moves away from the ideal, its utility
decreases into negative values. The more negative the utility (or
more positive the ``disutility''), the less useful the activity is for
the agent.
par
This disutility can be thought of as a monetary cost incurred from not
achieving all of the preferred timing goals for the activity. For
example, being late for work may result in a cut in pay, or an angry
boss, neither of which is good for the agent.
par
An activity's utility function is composed of three parts, according
to:
beginequation
utl_act = utl^T_b(t_b) + utl^T_e(t_e) + utl^T_d(t_d), labeleq:act-util-total
endequation
where
is, no plan is left out of consideration. Some agents will be sure
to use even the worst plans in their memory (which may or may not
improve their performance with successive tries).
par
item labelit:relax This cycle (i.e. steps refit:sim
through refit:select) is run for 150 times. Note that in the
last 50 cycles no new plans are created by the agents.
par
endenumerate
par
sectionUtility Functions for the Day Plan
labelsec:util-fcns
par
note Explain the problem
par
When the activities generator module generates the timing for the
activity schedule, it optimizes over the emphentire day all at
once, not piece-by-piece. This is to allow trade-offs between the
different parts of the day. For example, if the day has a large
number of activities that need to be accomplished, the activities
generator module should be able to do something like shorten the first
activity (i.e. leave home earlier) in order to fit the extra
activities at the end of the day. It should consider the travel-times
of the trips between the activities when scheduling them as well, so
as not to waste more time than necessary driving around. This might
mean temporally grouping activities that are geographically near one
another to avoid driving across town more times than necessary.
par
The module must solve a problem similar to, but not the same as,
departure time choice. One difference is that departure time choice
makes decisions for each trip independently from one another
citepMETROPOLIS, rather than allowing trade-offs between them.
Also, while the activity durations chosen by the activities generation
module directly effect the departure times of the agents' trips, those
departure times are not fixed. If, for example, an agent arrives late
to one activity, the agent will stay at the activity for the chosen
duration, rather than leaving early to stick to the departure time of
the next trip. In essence, priority is given to the timing of
activities over timing of trips, since the activities motivate the
trips, and not the other way around.
par
yy in a future version of this paper, this needs to be explained
better. we should explain what is the output of the time choice
module, and how the usim deals with it.
par
We were unable to find a single reference where we could look up a
meaningful set of utility functions to implement. As a result our
group has implemented two prototypes of activities generators with
their inclusive utility functions. The more ``diligent'' module of
the two, by D. Charypar, was not completed in time to use for this
study, but it will be presented at IATBR citepga4acts. Instead,
this work uses the simpler module by A. Schneider, which is described
here and elsewhere in this paper citepSchneider:act-times.
par
note Utility
par
In order for the activities generation module to calculate the optimal
day plan for an agent, it must have some way to evaluate the plan.
The utility function provides a way to do this by describing the
utility, or usefulness, the plan has to the agent (if the plan is not
useful, why would the agent execute it?). The utility function
translates the layout of the plan into a numerical value, which can be
thought of as a score or an actual value in monetary terms.
par
The utility of the day plan must incorporate the utilities for each
component of the plan. Those seperate utilities must be set relative
to one another so that they can be compared appropriately when making
trade-offs. In other words, changing a parameter of a more important
activity by a certain amount should effect the total utility more than
more than the same change on a less important activity.
par
Since location choice is currently not implemented, the different
activity types are differentiated only by their timing information.
In the utility function used for this paper, each activity type has a
preferred duration, and preferred time windows for when agents should
begin and end activities of that type. Different agents could have
different preferences for a given activity type, but in the current
implementation we give identical preferences to all agents.
par
Not all preferences of all activities in a day's plan can necessarily
be met, so the activity generator's job is to find the best compromise
between the specifications of each activity in order to make the whole
day as useful as possible to the agent.
par
The utility of the day plan measures the usefulness of that plan, or
how well it meets the needs of the agent. It is just the sum of the
utilities of each activity, plus the utilities of each trip. These
calculations are explained next.
par
subsectionUtility of a Single Activity
par
The utility function for a single activity measures how closely an
activity of a certain type (e.g. home or work) matches the preferences
set for that type.
par
An ``ideal'' instance of an activity would achieve the maximum
utility, which we set to 0.
As an activity instance moves away from the ideal, its utility
decreases into negative values. The more negative the utility (or
more positive the ``disutility''), the less useful the activity is for
the agent.
par
This disutility can be thought of as a monetary cost incurred from not
achieving all of the preferred timing goals for the activity. For
example, being late for work may result in a cut in pay, or an angry
boss, neither of which is good for the agent.
par
An activity's utility function is composed of three parts, according
to:
beginequation
utl_act = utl^T_b(t_b) + utl^T_e(t_e) + utl^T_d(t_d), labeleq:act-util-total
endequation
where
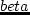 is the total utility for the activity;
is the total utility for the activity;
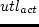 is the utility of the beginning time (
is the utility of the beginning time (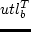 ) for an activity
of type
) for an activity
of type 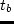 ;
;
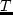 is the utility of the ending time (
is the utility of the ending time (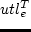 ) for an activity
of type
) for an activity
of type 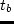 ;
and
;
and
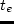 is the utility of the duration (
is the utility of the duration (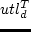 ) for an activity
of type
) for an activity
of type 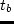 .
par
note modeling strategy
par
The next question is how to model the separate contributions. In this
early version of our utility model, we use piecewise linear functions
for mismatches at the activity starting and ending times, and a
quadratic function for deviations from the optimal activity duration.
Piecewise linear functions for the starting/ending times make sense
because (1) they allow direct modeling of the Vickrey model
citepArnott:etc:bottleneck, and because (2) piecewise linear
functions with enough pieces allow the modeling of nearly any
functional form. However, for the duration it was decided to use a
quadratic function because the piecewise linear approach causes too
many artifacts when competing with the piecewise linear contributions
of the starting/ending times mismatches. In the future, we intend to
use logarithmic utilities of duration instead citega4acts.
par
note Begin Time
par
The begin time utility,
.
par
note modeling strategy
par
The next question is how to model the separate contributions. In this
early version of our utility model, we use piecewise linear functions
for mismatches at the activity starting and ending times, and a
quadratic function for deviations from the optimal activity duration.
Piecewise linear functions for the starting/ending times make sense
because (1) they allow direct modeling of the Vickrey model
citepArnott:etc:bottleneck, and because (2) piecewise linear
functions with enough pieces allow the modeling of nearly any
functional form. However, for the duration it was decided to use a
quadratic function because the piecewise linear approach causes too
many artifacts when competing with the piecewise linear contributions
of the starting/ending times mismatches. In the future, we intend to
use logarithmic utilities of duration instead citega4acts.
par
note Begin Time
par
The begin time utility, 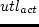 , is a piecewise linear function
incorporating a preferred window of time to begin the activity, and
penalties for starting too early or too late. The function looks
like:
beginequation
utl^T_b(t_b) = left{
beginarrayll
-a^T(t^a_b - t_b) & textrmif
, is a piecewise linear function
incorporating a preferred window of time to begin the activity, and
penalties for starting too early or too late. The function looks
like:
beginequation
utl^T_b(t_b) = left{
beginarrayll
-a^T(t^a_b - t_b) & textrmif
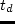 ,
,
-b^T(t_b - t^a_b) & textrmif
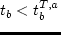 ,
,
0 & textrmelse.
endarray
right., labeleq:util-begin-end
endequation
where 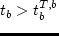 ,
, 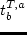 ,
, 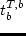 and
and 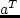 are the paramters that
describe the function for the given activity type
are the paramters that
describe the function for the given activity type 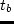 .
The values of
.
The values of 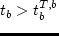 and
and 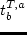 define the left and right
boundaries, respectively, of the preferred window of time for starting
the activity. If the starting time is within this window, there is no
penalty, so this part of the utility is 0, the ``ideal'' value. The
values of
define the left and right
boundaries, respectively, of the preferred window of time for starting
the activity. If the starting time is within this window, there is no
penalty, so this part of the utility is 0, the ``ideal'' value. The
values of 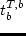 and
and 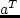 are the penalty rates for starting early or
late, respectively. The higher
are the penalty rates for starting early or
late, respectively. The higher 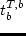 or
or 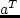 , the worse it is to be early
or late.
par
note End Time
par
The utility of the ending time for an activity looks just like the
utility for beginning the activity.
par
note Duration
par
The utility for the activity duration is calculated in a different
way. We use a quadratic formula, like so:
beginequation
utl^T_d(t_d) = -10 left( alpha^T ( t_d / t^T_d - 1 )right)^2,
labeleq:util-duration
endequation
where
, the worse it is to be early
or late.
par
note End Time
par
The utility of the ending time for an activity looks just like the
utility for beginning the activity.
par
note Duration
par
The utility for the activity duration is calculated in a different
way. We use a quadratic formula, like so:
beginequation
utl^T_d(t_d) = -10 left( alpha^T ( t_d / t^T_d - 1 )right)^2,
labeleq:util-duration
endequation
where
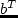 is a parameter describing the preferred duration for an
activity of type
is a parameter describing the preferred duration for an
activity of type 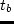 , and
, and 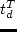 is a parameter that adjusts the
steepness of activity type
is a parameter that adjusts the
steepness of activity type 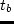 's parabola: higher values of
's parabola: higher values of 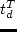 mean a faster penalty increase penalty for spending too much or not
enough time at the activity.
par
In this study we only use home and work activities. Their utility
functions are illustrated in Figures reffig:home-util-fcns
and reffig:work-util-fcns, respectively.
par
beginfigurebegincentercaptionHome activity utility functions.
Higher values are better (the highest possible value is 0).
pThe home (or essentially ``sleep'') activity starts at night,
after work, and continues through the night until morning. This
makes it appear as if the times of the begin and end functions are
reversed.
The preferred time to arrive (start) home is before midnight.
There is no penalty for getting home early, but arriving after
midnight causes the agent lose sleep, so the utility goes down.
The preferred time to leave (end) home is after 7:00 AM. It's
okay to leave anytime after that, but before then the agent loses
sleep so the score gets lower.
The preferred duration of home time is 16 hours. Since this
activity overlaps the day boundary, the start and end are
reversed. For this activity, the duration really means the agent
prefers to stay home
mean a faster penalty increase penalty for spending too much or not
enough time at the activity.
par
In this study we only use home and work activities. Their utility
functions are illustrated in Figures reffig:home-util-fcns
and reffig:work-util-fcns, respectively.
par
beginfigurebegincentercaptionHome activity utility functions.
Higher values are better (the highest possible value is 0).
pThe home (or essentially ``sleep'') activity starts at night,
after work, and continues through the night until morning. This
makes it appear as if the times of the begin and end functions are
reversed.
The preferred time to arrive (start) home is before midnight.
There is no penalty for getting home early, but arriving after
midnight causes the agent lose sleep, so the utility goes down.
The preferred time to leave (end) home is after 7:00 AM. It's
okay to leave anytime after that, but before then the agent loses
sleep so the score gets lower.
The preferred duration of home time is 16 hours. Since this
activity overlaps the day boundary, the start and end are
reversed. For this activity, the duration really means the agent
prefers to stay home 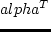 hours, corresponding to 8 hours
of sleep. Less sleep than this becomes quadratically worse.
labelfig:home-util-fcns
vspace1em
hrule
vspace1em
subfigure[Home begin time]includegraphics[width=0.3hsize]utl_h-begin-gz.epslabelfig:utl_h-beginsubfigure[Home end time]includegraphics[width=0.3hsize]utl_h-end-gz.epslabelfig:utl_h-endsubfigure[Home duration]includegraphics[width=0.3hsize]utl_h-dur-gz.epslabelfig:utl_h-durendcenter
hrule
endfigure
par
beginfigurebegincentercaptionWork activity utility functions.
Higher values are better (the highest possible value is 0). Slope
of 99 means that time must be adhered to; slope of 10 means it's
not preferred, but possible. Slope of 0 means anything goes.
The preferred time to begin work is between 7:00 AM and 9:00 AM.
Arriving earlier than 7 means some sleep was lost, so it has
disutility of 10 utility units per hour. Arriving to work after 9 is very
bad (99 units per hour) because the boss gets angry.
The preferred time to end work is between 4:00 PM and 6:00 PM;
it's very bad to leave early (boss), and it's not preferred by the
agent to leave late.
The preferred duration of work time is 8 hours; near 8 hours is
okay; the farther the duration is from 8 hours, the worse the
utility becomes, quadratically.
labelfig:work-util-fcns
vspace1em
hrule
vspace1em
subfigure[Work begin time]includegraphics[width=0.3hsize]utl_w-begin-gz.epslabelfig:utl_w-beginsubfigure[Work end time]includegraphics[width=0.3hsize]utl_w-end-gz.epslabelfig:utl_w-endsubfigure[Work duration]includegraphics[width=0.3hsize]utl_w-dur-gz.epslabelfig:utl_w-durendcenter
hrule
endfigure
par
subsectionUtility of the day plan
par
The total utility of the day plan is computed as the sum of all
individual utility contributions emphplus a disutility for the time
spent moving from one activity to another. This is to make sure
there is a trade-off between driving duration and activity durations.
For example, a worker might stay at work longer to avoid getting into
rush-hour traffic on its his way home.
To achieve this trade-off, time must also be translated into utility.
We use linear transformation, known as the value of time. Since no
effort was made to calibrate the utilities of the single activities,
at this point the value of time is just an arbitrary free parameter.
The next section will show some parametric studies as to the effect of
changing this parameter. Again, future versions of the time choice
module will contain more diligent values for all the free parameters.
par
sectionValidation Scenario
labelsec:test-case
par
To test the activities planning module with the feedback/learning
system, we implemented a simple scenario with plans containing only a
few parameters that are changeable by the agents, so we might be able
to follow the agents' decision-making.
par
subsectionThe Equil-Test Network
par
The scenario uses a simple network as shown in
fig. reffig:equil-test-net. In this network, there is just one
``home'' location and one ``work'' location. There are nine different
but identically long routes from home to work, and just one route from
work to home. With no network congestion, the free-speed travel-time
from home to work is 15 min (for all routes), and the travel-time from
work back to home is 39 min.
par
beginfigure
begincenter
captionThe equil-test network. Nodes (intersections) are the numbered circles. Links (roads) are
unidirectional; arrows show direction and line width indicates link
capacity. All links have a free speed of 100 km/h.
Most links are the same length (10 km), except the nine leading into
node 12 (5 km), and the long link connecting node 14 to 15 at the
bottom (35 km).
For clarity the different routes from home to work are drawn with
links of different lengths, but to the simulation the routes are all
identical in length.
Home and work locations are effectively at the end of their
respective link, but are still behind the capacity barrier of the
link.
labelfig:equil-test-net
vspace1em
hrule
vspace1em
includegraphics[width=0.9hsize]equil-test.net-fig.eps
endcenter
hrule
endfigure
par
For this scenario, we generate 2,000 agents with ``home-work-home''
day plans utilizing the above network. Initially, all agents have the
same plan: leave home at 6:00 AM and drive to work via node 7, then
stay at work for 8 hours and return home (via the only possible
route). Note that 6:00 AM, even with travel time added, is earlier
than the preferred time to start work, which is between 7:00 AM and
9:00 AM, as described Sec. refsec:util-fcns
(Fig. reffig:utl_w-begin). Using the activities replanning module
and the routing module, an agent can alter exactly three parts of its
plan: the departure time from home, the route used to get to work, and
the duration of the work activity.
par
The purpose of this scenario is to test the feedback system to make
sure the agents will improve their plans until the system has relaxed
into an approximate Nash Equilibrium. We expect the agents to adjust
their activity plans to leave home later, so they do not arrive to
work too early. We also expect the agents to adjust their routes to
avoid congestion as much as possible, as they did with the previous
version of the feedback system. Since all routes from home to work
are equivalent, equal numbers of agents should use each of the nine
routes.
par
The initial plans file is given to the simulation system described
above, and run for 150 iterations. Recall that the first 100
iterations follow the usual relaxation scheme, but during the last 50
iterations the agents are not allowed to create new plans; they can
only choose between the plans they have already tried.
par
As mentioned in Sec. refsec:util-fcns, the optimal value (or
disutility rate) of travel time is not known relative to the other
utility function parameters. So, the scenario is executed several
times with different values of time (0, 50, 500, 1500). As a control,
each version of the scenario is also run in a ``route-only'' mode,
where activities replanning is disabled. This leads to 8 versions of
the scenario.
par
subsectionRelaxation
par
In previous work, we looked at the sum of travel times as a measure of
the relaxation of the system. At that time, when the system performed
only route-replanning, the travel time of a trip was effectively the
score of the strategy. Now we want to include activity scheduling in
the measurement, so we look at the sum of the scores of the plans as
the measure of relaxation.
par
Figure reffig:relaxation shows the total score of all agents in the
system as a function of iteration (note: higher is better). One can
see that most of the relaxation happens quickly, in the first 20-30
iterations, then improvement slows down toward iteration 100. The
last 50 iterations do not change very much, except for fluctuations;
this is expected since no new plans are created, so improvement can
only come from plan selection. If the system is in an approximate
Nash Equilibrium, changing one agent's plan should not improve that
agent's score significantly. The figure seems to support this.
par
beginfigure
begincenter
captionRelaxation of runs with different values of time.
Top left: Value of time = 0.
Top right: Value of time = 50.
Bottom left: Value of time = 500.
Bottom right: Value of time = 1500.
labelfig:relaxation
vspace1em
hrule
vspace1em
includegraphics[width=0.4hsize]relaxation_vot0-gpl.eps
includegraphics[width=0.4hsize]relaxation_vot50-gpl.eps
includegraphics[width=0.4hsize]relaxation_vot500-gpl.eps
includegraphics[width=0.4hsize]relaxation_vot1500-gpl.eps
endcenter
hrule
endfigure
par
One also sees that with the activities replanning disabled
(``route-only''), the system always has a worse total score than with
activities replaning. This makes sense, since the initial activities
timing was not a very good one, and agents can not alter it. Their
only choice is which route to take to work. For lower values of time
the relaxation occurs in the direction of a worse total score! This
means that the initial plans (which all used the same route) were
better than the more distributed plans from later iterations. This
happens because the penalty for arriving to work so early (and thus
leaving work early) outweighs the advantage of having a faster route.
Since 10% of the agents are always replanned and the router always
generates the fastest route possible, the travel-times get shorter
with more iterations, making the arrival to work even earlier, which
makes the scores worse! Once the value of time is high enough, the
agents do benefit from shorter travel times, and are able to relax
toward better scores.
par
subsectionActivity Timing
par
If the scenario contained only one agent, that agent would never
encounter congestion and would have completely predictable travel
times. It is thus possible to analytically compute the best-scoring
plan possible for a single agent in the system. The best plan, to the
nearest second is: departure from home between 07:55:48 (hh:mm:ss) AM and
08:45:00 AM, and work duration of exactly 07:49:12 hours.
par
For 2000 agents, they cannot all follow the single best solution
because they would get in each others' way while implementing it. The
feedback system and agent database help the agents explore until they
find a good set of solutions to try out, which take into account the
usage of the network by the other agents.
par
All agents use the same utility functions. All have access to the
same information. The activity generation module supplies plans based
on complete information about network congestion obtained from the
previous simulation run. This means that within the decision phase of
a given iteration, every agent that requests a new activity plan will
receive the emphsame exact plan from the module. This is caused by
the property of the time choice module to always return the best
solution it has found so far, rather than, say, employing a discrete
choice model.
par
The result is that the agents leave home for work in several ``waves''
of home-to-work trips, and then leave work for home in a different set
of ``waves.'' One departure from home wave is of course the initial
06:00 AM departure, which some agents will always try out. These all
have 8 hour work durations, so including the home-to-work trip, they
lead to departures from work at about 2:15 PM.
par
Figure reffig:waves depicts these waves, showing how many agents
leave home or work during various 15-minute intervals throughout the
day. Most departures from home occur around 8:00 in the morning.
Since the agents have seperate routes from home to work, they are able
to spread out along these routes. For the departure from work, there
is only one route home, so the agents spread out so they are on the
road at different times by varying the duration of their work
activity. This effect is especially prominent at higher values of
time; in fact at higher values of time the travel time becomes so
significant that some agents choose to leave home emphbefore 6:00
AM.
par
beginfigure
begincenter
captionDeparture waves at various iterations for the scenarios with
activities planning enabled.
Morning times are departure times from home to work. Afternoon
times are departure times from work to home.
There are more departure waves leaving from work than from home.
As the value of time increases, the travel-times becomes more
important than the timing, so the departure times (esp. for leaving
work) spread out more to lower the time spent driving.
labelfig:waves
vspace1em
hrule
vspace1em
includegraphics[width=0.4hsize]histo_vot0-gpl.eps
includegraphics[width=0.4hsize]histo_vot50-gpl.eps
includegraphics[width=0.4hsize]histo_vot500-gpl.eps
includegraphics[width=0.4hsize]histo_vot1500-gpl.eps
endcenter
hrule
endfigure
par
The basic proportions between the times seems to be pretty consistent
between the different iterations.
par
subsectionRoute Equilibration
par
We expect that within a given ``wave'' of trips from home to work, the
agents will distribute themselves onto the nine identical routes
available to them. However, since the agents do not coordinate with
one another about who will take which route, they are not likely to be
perfectly balanced between the routes.
par
Figure reffig:route_histogram shows how the different routes
contribute to the departure waves seen in Fig. reffig:waves. The
routes appear to be used roughly equally, though there are some over-
and under-used routes. This seems to be caused by random
fluctuations.
par
beginfigure
begincenter
captionRoute equilibration for activities-replanned scenarios. A break-down of the routes used in the home-to-work departures from
Fig. reffig:waves. The ``boxes'' are emphstacked on top of
one another. That is, the visible portion of each ``box'' indicates
the relative number of agents using that route who departed within
that 15-minute time-bin; height of the individual boxes above the
x-axis axes is not relevant.
labelfig:route_histogram
vspace1em
hrule
vspace1em
includegraphics[width=0.4hsize]histo.route_vot0-gpl.eps
includegraphics[width=0.4hsize]histo.route_vot50-gpl.eps
includegraphics[width=0.4hsize]histo.route_vot500-gpl.eps
includegraphics[width=0.4hsize]histo.route_vot1500-gpl.eps
endcenter
hrule
endfigure
par
sectionDiscussion and Future Work
labelsec:discussion
par
One wonders why the departure ``waves'' are so prominent and distinct,
rather than spread out about the ideal plan. Further investigation
reveals that this is caused by a low ``free-speed'' setting of the
time choice module, causing it to estimate 50 km/h ``free-speed'' for
trips to unknown locations or starting at unsampled times. In
contrast, the free speed for all links in the test network is
100 km/h, so sampling certain trips at certain times leads to speeds
faster than the ``free'' speed, thus causing the module to prefer to
use time-bins that have already been used, and to not try new time
bins. This will be improved in future versions.
par
yy use different rnd seeds each time time chooser is called
par
In addition, the time choice module, being a Genetic Algorithm (GA),
always returns the best solution that it knows, rather than selecting
according to an exponentially weighted probability as would be done in
discrete choice theory. On the other hand, just returning the optimum
rather than making a random choice is computationally considerably
more tractable. And a Genetic Algorithm, stopped after a short time,
will in general not even return the optimum, but some intermediate
result. It is an open question of future research how the
distribution of results returned from such a GA compares to the
distribution of results generated by a (computationally much more
expensive) random utility model.
par
yy dave Charypar: distributions of intermed solutions in GA??
par
note eventual goal of Switzerland/big-Zurich.
par
The goal of our work is to be able to run a scenario of a full 24-hour
simulation of all of Switzerland, including transit traffic, freight
traffic, and all modes of transportation. This will involve about
7.5 million travelers, and more than 20 million trips (including short
pedestrian trips, etc.).
par
A more short-term goal is a full 24-hour simulation of all of car
traffic in Switzerland. For this, we will have about 4.5 million car
trips. However, we have not yet met this goal; while we have been
able to run route-replanning on the morning peak time-period for all
of Switzerland, as of this writing we have not succeeded in running
the activities feedback on this large scenario. We hope to be able to
have results from this scenario by the time of the IATBR conference.
par
sectionSummary
labelsec:summary
par
The limitations of the 4-step process are well known. One alternative
is a completely agent-based simulation approach to travel forecasting.
In an agent-based approach, each traveler is represented individually
throughout the whole simulation system. The necessary modules for
such an approach are: synthetic population generation module, activity
generation module(s), mode choice/route module(s), traffic simulation
module, and finally a feedback/learning mechanism. To our knowledge,
no agent-based system is available that successfully and consistently
implements all these modules; TRANSIMS is maybe the closest existing
implementation.
par
In this paper, we investigate the integration of activity time choice,
route planner, traffic simulation, and feedback. The last three
together form an agent-based version of Dynamic Traffic Assignment
(DTA), which has been investigated in earlier papers. Activity time
choice now for the first time goes beyond DTA in our work and
integrates the first aspect of activity feedback. Activity time
choice is related to departure time choice, but it is more complicated
since it attempts to find times for a complete 24-hour day plan,
instead of just for a single activity.
par
The problem is solved by attaching a separate time choice module to
the DTA process. In each iteration, not only can agents select new
and supposedly better routes, but they also obtain new activity
times. These times are generated by a Genetic Algorithm (GA) that
uses the following information as input: For each agent, the activity
pattern and their locations; a utility function that is (at this
point) the same for every agent; and a global view of the travel times
between network locations as a function of the time-of-day.
par
The paper shows verification runs with a testing scenario. The system
behaves essentially as expected, but an artifact was discovered with
respect to the model's assumption about travel times for areas in
space-time for which no feedback information was available.
Essentially, the model very much over-estimated travel times where it
had no other information, leading to the effect that travelers
clustered in space-time regions instead of spreading out. This will be
improved in future versions. In addition, different values of time
for travel were tried out. While a zero value of time for travel
leads to artifacts in the sense that agents attempt to prolong travel
time in order not to be early at the work location, a too high value
of time for travel puts such a high weight on travel times that
schedule delay plays no longer a role and all agents spread out so
much that everybody is driving at free speed.
par
As said before, the results presented here are preliminary. The
ultimate goal is a real-world case study.
par
section*Acknowledgments
par
Special thanks go to Adrian Schneider for the activities generation
module, which was his semester project during the winter 2003/03
semester.
par
bibliographystyleiatbr
bibliographyref,kai,projects,xref
par
enddocument
hours, corresponding to 8 hours
of sleep. Less sleep than this becomes quadratically worse.
labelfig:home-util-fcns
vspace1em
hrule
vspace1em
subfigure[Home begin time]includegraphics[width=0.3hsize]utl_h-begin-gz.epslabelfig:utl_h-beginsubfigure[Home end time]includegraphics[width=0.3hsize]utl_h-end-gz.epslabelfig:utl_h-endsubfigure[Home duration]includegraphics[width=0.3hsize]utl_h-dur-gz.epslabelfig:utl_h-durendcenter
hrule
endfigure
par
beginfigurebegincentercaptionWork activity utility functions.
Higher values are better (the highest possible value is 0). Slope
of 99 means that time must be adhered to; slope of 10 means it's
not preferred, but possible. Slope of 0 means anything goes.
The preferred time to begin work is between 7:00 AM and 9:00 AM.
Arriving earlier than 7 means some sleep was lost, so it has
disutility of 10 utility units per hour. Arriving to work after 9 is very
bad (99 units per hour) because the boss gets angry.
The preferred time to end work is between 4:00 PM and 6:00 PM;
it's very bad to leave early (boss), and it's not preferred by the
agent to leave late.
The preferred duration of work time is 8 hours; near 8 hours is
okay; the farther the duration is from 8 hours, the worse the
utility becomes, quadratically.
labelfig:work-util-fcns
vspace1em
hrule
vspace1em
subfigure[Work begin time]includegraphics[width=0.3hsize]utl_w-begin-gz.epslabelfig:utl_w-beginsubfigure[Work end time]includegraphics[width=0.3hsize]utl_w-end-gz.epslabelfig:utl_w-endsubfigure[Work duration]includegraphics[width=0.3hsize]utl_w-dur-gz.epslabelfig:utl_w-durendcenter
hrule
endfigure
par
subsectionUtility of the day plan
par
The total utility of the day plan is computed as the sum of all
individual utility contributions emphplus a disutility for the time
spent moving from one activity to another. This is to make sure
there is a trade-off between driving duration and activity durations.
For example, a worker might stay at work longer to avoid getting into
rush-hour traffic on its his way home.
To achieve this trade-off, time must also be translated into utility.
We use linear transformation, known as the value of time. Since no
effort was made to calibrate the utilities of the single activities,
at this point the value of time is just an arbitrary free parameter.
The next section will show some parametric studies as to the effect of
changing this parameter. Again, future versions of the time choice
module will contain more diligent values for all the free parameters.
par
sectionValidation Scenario
labelsec:test-case
par
To test the activities planning module with the feedback/learning
system, we implemented a simple scenario with plans containing only a
few parameters that are changeable by the agents, so we might be able
to follow the agents' decision-making.
par
subsectionThe Equil-Test Network
par
The scenario uses a simple network as shown in
fig. reffig:equil-test-net. In this network, there is just one
``home'' location and one ``work'' location. There are nine different
but identically long routes from home to work, and just one route from
work to home. With no network congestion, the free-speed travel-time
from home to work is 15 min (for all routes), and the travel-time from
work back to home is 39 min.
par
beginfigure
begincenter
captionThe equil-test network. Nodes (intersections) are the numbered circles. Links (roads) are
unidirectional; arrows show direction and line width indicates link
capacity. All links have a free speed of 100 km/h.
Most links are the same length (10 km), except the nine leading into
node 12 (5 km), and the long link connecting node 14 to 15 at the
bottom (35 km).
For clarity the different routes from home to work are drawn with
links of different lengths, but to the simulation the routes are all
identical in length.
Home and work locations are effectively at the end of their
respective link, but are still behind the capacity barrier of the
link.
labelfig:equil-test-net
vspace1em
hrule
vspace1em
includegraphics[width=0.9hsize]equil-test.net-fig.eps
endcenter
hrule
endfigure
par
For this scenario, we generate 2,000 agents with ``home-work-home''
day plans utilizing the above network. Initially, all agents have the
same plan: leave home at 6:00 AM and drive to work via node 7, then
stay at work for 8 hours and return home (via the only possible
route). Note that 6:00 AM, even with travel time added, is earlier
than the preferred time to start work, which is between 7:00 AM and
9:00 AM, as described Sec. refsec:util-fcns
(Fig. reffig:utl_w-begin). Using the activities replanning module
and the routing module, an agent can alter exactly three parts of its
plan: the departure time from home, the route used to get to work, and
the duration of the work activity.
par
The purpose of this scenario is to test the feedback system to make
sure the agents will improve their plans until the system has relaxed
into an approximate Nash Equilibrium. We expect the agents to adjust
their activity plans to leave home later, so they do not arrive to
work too early. We also expect the agents to adjust their routes to
avoid congestion as much as possible, as they did with the previous
version of the feedback system. Since all routes from home to work
are equivalent, equal numbers of agents should use each of the nine
routes.
par
The initial plans file is given to the simulation system described
above, and run for 150 iterations. Recall that the first 100
iterations follow the usual relaxation scheme, but during the last 50
iterations the agents are not allowed to create new plans; they can
only choose between the plans they have already tried.
par
As mentioned in Sec. refsec:util-fcns, the optimal value (or
disutility rate) of travel time is not known relative to the other
utility function parameters. So, the scenario is executed several
times with different values of time (0, 50, 500, 1500). As a control,
each version of the scenario is also run in a ``route-only'' mode,
where activities replanning is disabled. This leads to 8 versions of
the scenario.
par
subsectionRelaxation
par
In previous work, we looked at the sum of travel times as a measure of
the relaxation of the system. At that time, when the system performed
only route-replanning, the travel time of a trip was effectively the
score of the strategy. Now we want to include activity scheduling in
the measurement, so we look at the sum of the scores of the plans as
the measure of relaxation.
par
Figure reffig:relaxation shows the total score of all agents in the
system as a function of iteration (note: higher is better). One can
see that most of the relaxation happens quickly, in the first 20-30
iterations, then improvement slows down toward iteration 100. The
last 50 iterations do not change very much, except for fluctuations;
this is expected since no new plans are created, so improvement can
only come from plan selection. If the system is in an approximate
Nash Equilibrium, changing one agent's plan should not improve that
agent's score significantly. The figure seems to support this.
par
beginfigure
begincenter
captionRelaxation of runs with different values of time.
Top left: Value of time = 0.
Top right: Value of time = 50.
Bottom left: Value of time = 500.
Bottom right: Value of time = 1500.
labelfig:relaxation
vspace1em
hrule
vspace1em
includegraphics[width=0.4hsize]relaxation_vot0-gpl.eps
includegraphics[width=0.4hsize]relaxation_vot50-gpl.eps
includegraphics[width=0.4hsize]relaxation_vot500-gpl.eps
includegraphics[width=0.4hsize]relaxation_vot1500-gpl.eps
endcenter
hrule
endfigure
par
One also sees that with the activities replanning disabled
(``route-only''), the system always has a worse total score than with
activities replaning. This makes sense, since the initial activities
timing was not a very good one, and agents can not alter it. Their
only choice is which route to take to work. For lower values of time
the relaxation occurs in the direction of a worse total score! This
means that the initial plans (which all used the same route) were
better than the more distributed plans from later iterations. This
happens because the penalty for arriving to work so early (and thus
leaving work early) outweighs the advantage of having a faster route.
Since 10% of the agents are always replanned and the router always
generates the fastest route possible, the travel-times get shorter
with more iterations, making the arrival to work even earlier, which
makes the scores worse! Once the value of time is high enough, the
agents do benefit from shorter travel times, and are able to relax
toward better scores.
par
subsectionActivity Timing
par
If the scenario contained only one agent, that agent would never
encounter congestion and would have completely predictable travel
times. It is thus possible to analytically compute the best-scoring
plan possible for a single agent in the system. The best plan, to the
nearest second is: departure from home between 07:55:48 (hh:mm:ss) AM and
08:45:00 AM, and work duration of exactly 07:49:12 hours.
par
For 2000 agents, they cannot all follow the single best solution
because they would get in each others' way while implementing it. The
feedback system and agent database help the agents explore until they
find a good set of solutions to try out, which take into account the
usage of the network by the other agents.
par
All agents use the same utility functions. All have access to the
same information. The activity generation module supplies plans based
on complete information about network congestion obtained from the
previous simulation run. This means that within the decision phase of
a given iteration, every agent that requests a new activity plan will
receive the emphsame exact plan from the module. This is caused by
the property of the time choice module to always return the best
solution it has found so far, rather than, say, employing a discrete
choice model.
par
The result is that the agents leave home for work in several ``waves''
of home-to-work trips, and then leave work for home in a different set
of ``waves.'' One departure from home wave is of course the initial
06:00 AM departure, which some agents will always try out. These all
have 8 hour work durations, so including the home-to-work trip, they
lead to departures from work at about 2:15 PM.
par
Figure reffig:waves depicts these waves, showing how many agents
leave home or work during various 15-minute intervals throughout the
day. Most departures from home occur around 8:00 in the morning.
Since the agents have seperate routes from home to work, they are able
to spread out along these routes. For the departure from work, there
is only one route home, so the agents spread out so they are on the
road at different times by varying the duration of their work
activity. This effect is especially prominent at higher values of
time; in fact at higher values of time the travel time becomes so
significant that some agents choose to leave home emphbefore 6:00
AM.
par
beginfigure
begincenter
captionDeparture waves at various iterations for the scenarios with
activities planning enabled.
Morning times are departure times from home to work. Afternoon
times are departure times from work to home.
There are more departure waves leaving from work than from home.
As the value of time increases, the travel-times becomes more
important than the timing, so the departure times (esp. for leaving
work) spread out more to lower the time spent driving.
labelfig:waves
vspace1em
hrule
vspace1em
includegraphics[width=0.4hsize]histo_vot0-gpl.eps
includegraphics[width=0.4hsize]histo_vot50-gpl.eps
includegraphics[width=0.4hsize]histo_vot500-gpl.eps
includegraphics[width=0.4hsize]histo_vot1500-gpl.eps
endcenter
hrule
endfigure
par
The basic proportions between the times seems to be pretty consistent
between the different iterations.
par
subsectionRoute Equilibration
par
We expect that within a given ``wave'' of trips from home to work, the
agents will distribute themselves onto the nine identical routes
available to them. However, since the agents do not coordinate with
one another about who will take which route, they are not likely to be
perfectly balanced between the routes.
par
Figure reffig:route_histogram shows how the different routes
contribute to the departure waves seen in Fig. reffig:waves. The
routes appear to be used roughly equally, though there are some over-
and under-used routes. This seems to be caused by random
fluctuations.
par
beginfigure
begincenter
captionRoute equilibration for activities-replanned scenarios. A break-down of the routes used in the home-to-work departures from
Fig. reffig:waves. The ``boxes'' are emphstacked on top of
one another. That is, the visible portion of each ``box'' indicates
the relative number of agents using that route who departed within
that 15-minute time-bin; height of the individual boxes above the
x-axis axes is not relevant.
labelfig:route_histogram
vspace1em
hrule
vspace1em
includegraphics[width=0.4hsize]histo.route_vot0-gpl.eps
includegraphics[width=0.4hsize]histo.route_vot50-gpl.eps
includegraphics[width=0.4hsize]histo.route_vot500-gpl.eps
includegraphics[width=0.4hsize]histo.route_vot1500-gpl.eps
endcenter
hrule
endfigure
par
sectionDiscussion and Future Work
labelsec:discussion
par
One wonders why the departure ``waves'' are so prominent and distinct,
rather than spread out about the ideal plan. Further investigation
reveals that this is caused by a low ``free-speed'' setting of the
time choice module, causing it to estimate 50 km/h ``free-speed'' for
trips to unknown locations or starting at unsampled times. In
contrast, the free speed for all links in the test network is
100 km/h, so sampling certain trips at certain times leads to speeds
faster than the ``free'' speed, thus causing the module to prefer to
use time-bins that have already been used, and to not try new time
bins. This will be improved in future versions.
par
yy use different rnd seeds each time time chooser is called
par
In addition, the time choice module, being a Genetic Algorithm (GA),
always returns the best solution that it knows, rather than selecting
according to an exponentially weighted probability as would be done in
discrete choice theory. On the other hand, just returning the optimum
rather than making a random choice is computationally considerably
more tractable. And a Genetic Algorithm, stopped after a short time,
will in general not even return the optimum, but some intermediate
result. It is an open question of future research how the
distribution of results returned from such a GA compares to the
distribution of results generated by a (computationally much more
expensive) random utility model.
par
yy dave Charypar: distributions of intermed solutions in GA??
par
note eventual goal of Switzerland/big-Zurich.
par
The goal of our work is to be able to run a scenario of a full 24-hour
simulation of all of Switzerland, including transit traffic, freight
traffic, and all modes of transportation. This will involve about
7.5 million travelers, and more than 20 million trips (including short
pedestrian trips, etc.).
par
A more short-term goal is a full 24-hour simulation of all of car
traffic in Switzerland. For this, we will have about 4.5 million car
trips. However, we have not yet met this goal; while we have been
able to run route-replanning on the morning peak time-period for all
of Switzerland, as of this writing we have not succeeded in running
the activities feedback on this large scenario. We hope to be able to
have results from this scenario by the time of the IATBR conference.
par
sectionSummary
labelsec:summary
par
The limitations of the 4-step process are well known. One alternative
is a completely agent-based simulation approach to travel forecasting.
In an agent-based approach, each traveler is represented individually
throughout the whole simulation system. The necessary modules for
such an approach are: synthetic population generation module, activity
generation module(s), mode choice/route module(s), traffic simulation
module, and finally a feedback/learning mechanism. To our knowledge,
no agent-based system is available that successfully and consistently
implements all these modules; TRANSIMS is maybe the closest existing
implementation.
par
In this paper, we investigate the integration of activity time choice,
route planner, traffic simulation, and feedback. The last three
together form an agent-based version of Dynamic Traffic Assignment
(DTA), which has been investigated in earlier papers. Activity time
choice now for the first time goes beyond DTA in our work and
integrates the first aspect of activity feedback. Activity time
choice is related to departure time choice, but it is more complicated
since it attempts to find times for a complete 24-hour day plan,
instead of just for a single activity.
par
The problem is solved by attaching a separate time choice module to
the DTA process. In each iteration, not only can agents select new
and supposedly better routes, but they also obtain new activity
times. These times are generated by a Genetic Algorithm (GA) that
uses the following information as input: For each agent, the activity
pattern and their locations; a utility function that is (at this
point) the same for every agent; and a global view of the travel times
between network locations as a function of the time-of-day.
par
The paper shows verification runs with a testing scenario. The system
behaves essentially as expected, but an artifact was discovered with
respect to the model's assumption about travel times for areas in
space-time for which no feedback information was available.
Essentially, the model very much over-estimated travel times where it
had no other information, leading to the effect that travelers
clustered in space-time regions instead of spreading out. This will be
improved in future versions. In addition, different values of time
for travel were tried out. While a zero value of time for travel
leads to artifacts in the sense that agents attempt to prolong travel
time in order not to be early at the work location, a too high value
of time for travel puts such a high weight on travel times that
schedule delay plays no longer a role and all agents spread out so
much that everybody is driving at free speed.
par
As said before, the results presented here are preliminary. The
ultimate goal is a real-world case study.
par
section*Acknowledgments
par
Special thanks go to Adrian Schneider for the activities generation
module, which was his semester project during the winter 2003/03
semester.
par
bibliographystyleiatbr
bibliographyref,kai,projects,xref
par
enddocument



Nächste Seite: Über dieses Dokument ...
Bryan Raney
2003-07-08