


Nächste Seite: Über dieses Dokument ...
documentclass[a4paper,10pt,oneside,onecolumn,titlepage,final]article
usepackage[a4paper,left=1.25in,right=1.25in,top=1in,bottom=1in]geometry
usepackagetimes
usepackagehelvet
usepackagetabularx
usepackagegraphicx
usepackageamssymb
usepackage[nooneline]caption
usepackagenatbib
usepackagefancyhdr
makeatletter
letKEEPheadruleheadrule
letheadruleundefined
letKEEPfootrulefootrule
letfootruleundefined
makeatother
usepackagetitlesec
titleformatsectionLargesffamilybfseriesthesection.1em
titleformatsubsectionlargesffamilybfseriesthesubsection1em
titleformatsubsubsectionnormalfontsffamilybfseriesthesubsubsection1em
par
titleformatparagraph[hang]normalfontsffamilybfseriesitshape0pt
par
titleformatsubparagraph[hang]smallsffamilybfseriesitshape0pt
usepackagegerman
selectlanguageUSenglish
letheadruleKEEPheadrule
letfootruleKEEPfootrule
par
pagestylefancy
lheadtextitInternational Conference on Travel Behaviour Research
rheadtextitAugust 10-14, 2003
par
setlengthparindent0in
setlengthparskip10pt
par
newedcommandmytitleGenerating Complete All-Day Activity Plansnewline with Genetic Algorithms
par
usepackagemarvosym
par
begindocument
par
begintitlepage
par
hrule
begincenter
includegraphics[width=0.7textwidth]map_full10_short_sp1-fig.eps
endcenter
hrule
par
sffamily
par
vspace0.5in centerLARGEtextbfmytitle
par
vspace0.5in Large
noindent textbfDavid Charypar, Dept. of Computer Science, ETH Zürich
noindent textbfKai Nagel, Dept. of Computer Science, ETH Zürich
par
par
vspace0.25in noindent textbflarge
textbflarge
par
sffamily
vspace0.25in
par
begintabular[b]cp5in
par
includegraphics[width=1.15in]iatbr_logo.eps.gzhspace0.1in & large
vspace-0.75in
textbfMoving through nets:newline
textbfThe physical and social dimensions of travelnewline
10
International Conference on Travel Behaviour Researchnewline
Lucerne, 10-14. August 2003
par
endtabular
par
par
vfilleject
setcounterpage1
par
vspace0.25in noindent textbfsffamilyLarge mytitle
par
bigskip
par
noindent
David Charypar
Department of Computer Science
ETH Zürich
CH-8092 Zürich, Switzerland
par
noindent
parbox[t]0.5inPhone: +41 (0)1 632 47 63
parbox[t]0.5inFax: +41 (0)1 632 13 74
parbox[t]0.5ineMail: charypar@inf.ethz.ch
par
bigskip
par
noindent
Kai Nagel
Department of Computer Science
ETH Zürich
CH-8092 Zürich, Switzerland
par
noindent parbox[t]0.5inPhone: +41 (0)1 632 27 54
parbox[t]0.5inFax: +41 (0)1 632 13 74
parbox[t]0.5ineMail: nagel@inf.ethz.ch
par
bigskip
par
noindent
textbfsffamilyLarge Abstract
par
noindent
The four step process generates demand via trip generation and trip
distribution. It is well known that this method has disadvantages
because it decouples trip distribution (and later steps) from
demographic information, and it is difficult to make it
time-dependent. An alternative is activity-based demand generation,
which contructs complete all-day activity plans for each member of a
population, and derives transportation demand from the fact that
consecutive activities at different locations need to be connected by
travel. Besides many other advantages, activity-based demand
generation also fits well into the paradigm of multi-agent simulation,
where each traveler is kept as an individual throughout the whole
modeling process.
par
Despite these advantages, there are unfortunately rather few
operational activity generation models, which can be used to actually
drive simulations. Being operational includes the capability to
actually generate fully specified plans (including patterns,
locations, and times), to be able to generate such plans for
population sizes of several millions, and to display sensitivity to
congestion.
par
In this paper, we present a new approach to the problem, which uses
genetic algorithms (GA). Our GA keeps, for each member of the
population, several instances of possible all-day activity plans in
memory. Those plans are modified by mutation and crossover, while
``bad'' instances are eventually discarded.
par
Any GA needs a fitness function to evaluate the performance of each
instance. For all-day activity plans, it makes sense to use a utility
function to obtain such a fitness. In consequence, a significant part
of the paper is spent discussing such a utility function. In
addition, the paper shows the performance of the algorithm to a few
selected problems, including very busy and rather non-busy days.
par
vfill
par
vspace0.25in noindent textbfsffamilyLarge Keywords
par
noindent Activity generation; Utility functions; Genetic Algorithms; Location
choice; Multi-agent traffic simulation
par
endtitlepage
sectionIntroduction
par
It is a recent trend in transportation research to use the problem of
activity planning in order to generate demand for transportation.
Transportation demand is naturally derived from performing activities
at different locations.
The larger context of this work is the push towards an integrated
multi-agent simulation model for transportation planning. Multi-agent
simulations can be employed on many levels, from housing choice down
to driving behavior. Our own initial goal is to replace the four-step
process by a multi-agent simulation. This implies the following
modules and methods:
beginitemize
par
item The process starts by generating a strc synthetic population
from census data. A synthetic population is a Monte-Carlo realization
of the information provided by the census data.
par
item Next, synthetic strc activity plans are generated for each
member of the population. This is the topic of this paper.
par
item Once the activity plans are known, each individual plans the
travel that connects activities at different locations, including
strc mode choice and strc route choice.
par
item Up to here, the computations of the agents are essentially
independent (apart from possible small-scale coordination problems
such as household coordination or ride sharing). In contrast, in the
strc traffic (micro-)simulation, all agents' plans are
simultaneously executed and the results of interaction are computed. One
important interaction result is congestion.
par
item As is well known, the causal relation between the modules goes
into both directions. For example, if many agents chose activities at
many different and far apart locations, then this will cause
congestion. This congestion will cause them to select activities
which necessitate less travel. The typical way to solve this problem
is to use strc iterations between the modules. This can be either
interpreted as relaxation or as human learning.
par
enditemize
par
In the context of such a simulation system, all plans need to be
specified in an unambiguous way so that the micro-simulation can
execute them.
In addition, since we are interested in large scale scenarios with up
to 10 mio agents, the computation of the plans should not need more
than a small number of seconds per agent.
par
Finally, multi-agent simulations for scenarios of that size use
parallel computing for computational speed. It is difficult to
implement within-day replanning in such a parallel system without
giving up parallel performance. For that reason, most if not all
large scale multi-agent transportation simulations at this point need
the complete all-day activity plan emphpre-planned before the
simulated day starts.
par
sectionProblem description
par
note Activity Planning as whole problem
par
The problem of activity planning is the task to generate a complete
activity plan for an agent from a set of possible activities. yy axh
hat eine Nomenklatur hier, die wir benutzen sollten. Kai In this
context, a complete activity plan is an activity plan that stores
which activities are to be executed and in which order, it assigns a
location to each activity and also an execution time and a duration.
par
note AP can be devided into three subproblems
Activity planning divides into three subproblems:
beginitemize
item The first subproblem is to select activities to be executed and to decide in
which order they should be executed. We refer to this subproblem as
emphactivity pattern generation.
item The second subproblem is to find the places where the activities are going
to be executed. We call this emphlocation selection. The location selection
has to fulfill a number of constraints in order to be meaningful. For instance
children should be fetched from school at the same place where they were
dropped off before.
item The third subproblem is to decide when the activities have to be
executed and for how long. We call this emphtime allocation. Once again, time
allocation is subject to several restrictions as well. The most simple one of
this is that the execution times should be ordered in correspondence with the
activity pattern.
enditemize
par
note Reality: we do ap every day
In reality, all of us do activity planning every day with sufficient
speed and satisfactory results.
note difficult on computer
Nevertheless this
problem is quite
difficult to solve automatically on the computer. The main problem
with activity planing is the huge amount of possible plans for
a given set of activities. Even if one is just concentrating on emphactivity
pattern generation for a list of ten activities, there are almost
10 million possible solutions.
It is clear that we get even more problems if we want to include
emphlocation selection and emphtime allocation.
par
note longer plans (week) would be better, because day plans depend on each other
To make the problem even worse, it would be desirable to extend the length
of the activity plan to a week or even a month because day plans are not
independent in general as some activities do not have to be executed every day.
For instance you do not have to go shopping every day, but you normally cannot
omit shopping for a longer period.
note longer plans make the problem even worse
Since the space for possible solutions scales exponentially with the length of
the desired activity plan, generating complete week plans is a problem that is
several orders of magnitude more complex than generating day plans.
par
note Importance for mobility simulations
par
note introduce agent based approach
par
sectionRelated work
par
There are many models tackling the same problem. One can maybe
differentiate the following directions:
beginitemize
par
item A possible way to solve this problem is to use a nested
multinomial logit model. One such system is described by
citetBowman:thesis. The decision is decomposed into many
hierarchical levels, such as: the choice between different activity
patterns, the choice between different locations, the choice between
different starting times for the patterns, etc. This method demands
that approximations of the lower level results are available at the
upper levels: For example, in order to decide between different
activity patterns, it is necessary to have a performance estimate for
each pattern, which can only be obtained if the algorithm has some
idea about the locations and times that will be chosen for each
pattern. In practice, this is achieved via the so-called logsum
terms, which backpropagate the lower level solutions to the higher
levels. That is, the algorithm starts at the leaves of the decision
tree. There, it computes, for each given activity pattern and
location choice, utilities for each possible time choice. It then
calculates the expected utility from this, and passes this on to the
location choice level. The location choice level then calculates, for
each given pattern, the expected utility for each location choice and
passes the resulting expected utility for each pattern one level up,
etc.
Once the algorithm is at the highest level, it selects between the
patterns according to the utilities. Once the pattern is selected,
for this given pattern it selects between the locations. Once the
locations are selected, it decides on the time-of-day when the pattern
is started.
par
Discrete choice models have a similar conceptual approach as our
model in that they make choices based on utilities. The two main
differences are that, at least conceptually, discrete choice models
enumerate emphall possible alternatives, and that they do not chose
the option with the best utility but they chose between options with
probabilities which are related to utilities. The first aspect means
that a huge number of options needs to be considered; the second
(behaviorally justified) aspect means that efficient search methods
such as branch-and-bound cannot be used because even ``bad'' branches
of the search tree have a probability that they will be selected.
par
item An arguably related approach is STARCHILD and successors.
Instead of making a probabilistic choice between different options, it
finds the optimal solution. Because of this simplification, methods
from mathematical programming can be applied citep[e.g.][]Recker.
par
item Both approaches mentioned so far always look at the complete
schedule. As an alternative, a traveler may build the schedule as
he/she goes. An extreme version of this is PCATS citep[e.g.][]PCATS, which
conditions decisions on the past history, but does not look into the
future. The advantage is much more manageable computational
complexity; the disadvantage is that the algorithm does not pick up
scheduling constraints which lie in the future.
par
item The work by Doherty and coworkers citep[e.g.][]Doherty:fvu
implies that real-world activity scheduling is a combination of the
above aspects, i.e. that some decisions are made a long time in
advance while others are rather spontaneous. An implementation of
this approach is ALBATROSS citep[e.g.][]ALBATROSS.
par
enditemize
Also, there are other micro-simulation models of human behavior, such
as URBANSIM citepURBANSIM or ILUTE citepILUTE, which at this point
concentrate on even higher level aspects, such as residential choice.
par
sectionIdea: Genetic Algorithms
labelsec:idea:-genet-algor
par
note Enumerating not possible; but also need not optimal solution
par
Trying to solve the problem by enumerating all possibilities--a
complete search--is infeasible. This is especially true if one has
only very limited computer time for program execution, as is the case
with large scale multi-agent implementations. Furthermore, for our
problem it is not absolutely necessary to find the global optimal
solution. In fact, in many cases what people use as their plan is
far from being optimal. It would be sufficient to find a ``good''
solution.
par
note Therefore, use GA
par
The idea for this paper is to use a Genetic Algorithm (GA) to find
good all-day activity plans.
GAs have been used for many problems with huge search spaces.
GAs maintain a population of solution instances during the search
process, and search progress is made by mutation, crossover, and
selection, as explained below. In our case, the members of the
population are represented by possible day plans for a single given traveler.
The quality of such a day plan is rated by a fitness function which
uses informations and restrictions known about the activities, and
estimates how well the day plan meets them.
par
A random population of such day plans is created at the beginning of
the algorithm and their quality rated as described above. All the generatad day
plans represent a possible day plan for the same traveller. New
individuals are created by crossover between two good day plans and
mutating the offspring. When new, better day plans are found, then the
worst plans are removed keeping allways a population of constant size.
This procedure is repeated a number oftimes.
At the end, the best day plan is used as solution of the problem.
par
Note that the work ``population'' is used with two different meanings
in this text: First, there is a population of travelers that populates
the multi-agent traffic simulation. But second, there is also a
population of solution instances within the GA. In the remainder of
the text, in general the second meaning will be used.
par
sectionImplementation par
As mentioned above, crossover, mutation and selection are vital
components of each GA.
Before these operators can be defined, it is
necessary to come up with a way of representing a solution instance
in the computer.
This way of representation is referred to as strc encoding.
Encoding is of prime importance for the definition of crossover and
mutation and it has a large influence on the potential performance of
a GA. That's why one should always spend some time in figuring out a
good encoding for one's problem before starting the definition of the
other operators.
par
For our problem of activity planning, we used a
combination of binary encoding, permutation encoding and value
encoding in the following way:
beginitemize
item
Each activity can be either included in the day plan or excluded from it. The
informations about inclusion of activities is stored in an array of bits, where
each bit holds this information for one activity. If a bit is set to one the
corresponding activity is included in the day plan, if it is set to zero the
corresponding activity is excluded from the plan.
item
A second array stores the order of the activities. It holds always a
full set of activities, regardless of which activities are actually
member of the day plan and which not. When evaluating the day plan,
the positions with disabled activities are ignored. See figure
reffig:pattern.
par
beginfigure
begincenter
includegraphics[width=0.5textwidth]pattern-fig.eps
caption[possible encoding of pattern ``241'']One possible encoding of the activity pattern ``241''
labelfig:pattern
endcenter
endfigure
par
item
Our day plans also include the informations about the location selection. In our
model we assume that there exists a facility that is assigned to each activity.
This facility can be thought of as a type of building or place that is needed in
order to perform the activity. For instance, for the activity ``go shopping'' we
would need the facility ``shop''. We do also assume that each facility exists at
multiple locations as for example there are multiple shops in a city where
shopping can be done. The concept of facilities makes it possible to have
locations of activities that depend on each other.
For instance, this is needed to take care of the fact that one has to fetch his
children at the same school as one has drooped them off before.
The day plan has to store the selected location for each facility.
This information is held in a third array.
par
item
The allocated time to the activities is stored in a fourth array which
stores floating point numbers; in addition, there is an entry which contains the
starting time of the day plan. Activity starting times of the
allocated time slots are a result of adding up the allocated times of
the previous activities of the day plan.
par
enditemize
par
note parent selection
par
The parents for a new individual are selected at random out of the
current population. That is, better day plans do emphnot have a
higher probability than worse day plans to reproduce themselves.
We did not want to prefer better day plans in parent
selection because we did not want to risk a too early degeneration of
the population. However, the introduction of a different parent
selection scheme, for example rank selection, could yield a faster
convergence. Recall from section refsec:idea:-genet-algor that
offspring is only kept when it is better than the currently worst
member of the population, and in that case, the worst member is
removed.
par
pagebreak
note crossover operator
The implementation of the textbfcrossover operator is built of three parts:
beginitemize
item First, the array which stores the membership information is processed
using uniform crossover. That is each flag is copied randomly from one of the
parents.
item Second, we crossover the arrays that store the order information in the
following way:
Before we start, we decide randomly which parent should precede in case of a
collision.
This information is needed during the rest of order crossover.
We create a temporary array to store the order information of the newly created
offspring.
This array is three times larger then necessary in order to provide enough
space for insertions of elements.
For each activity, we now randomly select a parent and put the activity at the
same position in the offspring as it was in the selected parent.
If the target position is already taken--this means that another activity was
copied earlier to this position--the new activity is inserted before or after
the already present activity, dependent on the precedence information from the
first step.
As a postprocessing step we remove the holes in the temporary array by copying
it to the final array.
par
yy Hier wäre wohl eine Zeichnung hilfreich. Dave. Finde ich auch. Kai
par
item Third, for each activity the time allocation is copied randomly from one
of the two parents.
enditemize
par
We believe that our implementation of the crossover operator has
several advantages compared to single point crossover. Single point
crossover is a very popular implementation of crossover. The
offspring is created from the parents by taking their representations,
choosing a random crossover point and copying the first part up to
this point from the first parent and the second part beginning at this
point from the second parent.
par
However, for sequencing problems such as ours, this approach does not
work since there is a large chance that in the offspring, some
activities will be performed twice while some others will have
completely vanished. A solution, coming from GA encoding for the
Traveling Salesman Problem, is to take the first part verbatim from
the first parent, and then to fill up the remaining spots with the
remaining activities in the sequence they are in the second parent,
skipping activities which are already present in order to avoid
duplicate activities in the offspring.
par
That encoding has however the disadvantage that it only looks at the
sequence and not at all at time-of-day. In contrast, in our
implementation, activities have a tendency to stay at their position
within the day plan. In addition,
our crossover operator shuffles the activities more than a single
point crossover would, and our tests showed that this yields a more
stable--although slower--convergence.
This is desirable, because our experience with GAs shows a considerable
tendency to keep stuck in local optima when using single point
crossover.
par
The textbfmutation operator is split into four parts:
First, for each activity, the membership information is flipped with a
probability 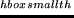 .
Second, the order of the activities is permuted.
With a probability
.
Second, the order of the activities is permuted.
With a probability 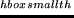 two activities, both chosen at random, are
exchanged.
This is done
two activities, both chosen at random, are
exchanged.
This is done 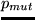 times where
times where 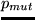 is the total number of activities.
Using the same idea as in the crossover operator, the activities are exchanged
ignoring the membership information.
Third, the time allocation of each activity is changed by multiplying it with a
factor
is the total number of activities.
Using the same idea as in the crossover operator, the activities are exchanged
ignoring the membership information.
Third, the time allocation of each activity is changed by multiplying it with a
factor 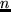 , where
, where 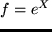 is drawn uniformly
from the interval
is drawn uniformly
from the interval
![$[-p_{mut}/2, p_{mut}/2]$](img6.png) .
Fourth, a new start time of the activity plan is calculated by adding a random
time uniformly drawn from
.
Fourth, a new start time of the activity plan is calculated by adding a random
time uniformly drawn from
![$[-p_{mut}cdot 12h, p_{mut}cdot 12h]$](img7.png) .
par
sectionUtility function
par
note fitness function
note make clear: assuming fitness is sum of utilities
par
As already mentioned earlier, our GA needs to rate the
quality of the day plans in the population. For that purpose one has
to define a emphfitness function which somehow defines what a
``good'' day plan is. We use a fitness function that is the
sum of the utilities of all activities that are performed.
beginequation
F = sum_i=1^n utility(type_i, start_i, dur_i, lastloc_i, loc_i)
endequation
Here,
.
par
sectionUtility function
par
note fitness function
note make clear: assuming fitness is sum of utilities
par
As already mentioned earlier, our GA needs to rate the
quality of the day plans in the population. For that purpose one has
to define a emphfitness function which somehow defines what a
``good'' day plan is. We use a fitness function that is the
sum of the utilities of all activities that are performed.
beginequation
F = sum_i=1^n utility(type_i, start_i, dur_i, lastloc_i, loc_i)
endequation
Here, 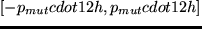 is the type of the activity,
is the type of the activity, 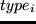 is the starting time of the
activity,
is the starting time of the
activity, 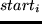 is the amount of time allocated to the activity,
is the amount of time allocated to the activity, 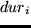 is the location of the last activity and
is the location of the last activity and 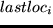 is the location of the current
activity. In the following part, we will discuss all aspects of our utility
function in detail.
par
In our model, the utility of an activity depends on the following parameters:
beginitemize
item The allocated time to the activity
item The time of day when the time slot for the activity starts
item The location where the activity takes place
item The location where the last activity took place.
enditemize
par
The total utility of an activity
is the location of the current
activity. In the following part, we will discuss all aspects of our utility
function in detail.
par
In our model, the utility of an activity depends on the following parameters:
beginitemize
item The allocated time to the activity
item The time of day when the time slot for the activity starts
item The location where the activity takes place
item The location where the last activity took place.
enditemize
par
The total utility of an activity 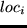 is the sum of five terms, each of
which is modeling a certain aspect of the utility function.
beginequation
U_total,i = U_travel,i + U_dur,i + U_wait,i + U_late.ar,i + U_early.dp,i
endequation
Here,
is the sum of five terms, each of
which is modeling a certain aspect of the utility function.
beginequation
U_total,i = U_travel,i + U_dur,i + U_wait,i + U_late.ar,i + U_early.dp,i
endequation
Here, 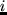 denotes the disutility of traveling from the last
location to the next one,
denotes the disutility of traveling from the last
location to the next one,
 denotes the utility of
executing the activity for a certain duration,
denotes the utility of
executing the activity for a certain duration,  denotes the
disutility of waiting (for instance waiting for a shop to open) and
denotes the
disutility of waiting (for instance waiting for a shop to open) and
 and
and
 denote penalties for coming too late
or leaving too early respectively.
par
The utility (
denote penalties for coming too late
or leaving too early respectively.
par
The utility (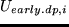 fitness) of the complete day plan is then given by
the sum of all utility contributions of all fitnesses:
beginequation
labeleq:utl
U_total = sum_i U_total,i .
endequation
Note that this has the consequence that when removing an activity, the
travel terms at emphboth ends are modified. That is, if an
activity is far out of the way, then dropping that activity will
reduce overall travel considerably, while dropping an activity that is
on the way will have a negligible effect on travel times.
par
In the following, the different terms and their parameters will be
discussed in detail.
All terms except
fitness) of the complete day plan is then given by
the sum of all utility contributions of all fitnesses:
beginequation
labeleq:utl
U_total = sum_i U_total,i .
endequation
Note that this has the consequence that when removing an activity, the
travel terms at emphboth ends are modified. That is, if an
activity is far out of the way, then dropping that activity will
reduce overall travel considerably, while dropping an activity that is
on the way will have a negligible effect on travel times.
par
In the following, the different terms and their parameters will be
discussed in detail.
All terms except  are linear in
the time needed for that
activity. Despite the detailed discussion, it should be kept in mind
that the technology of using a GA is entirely independent from the
specific utility function. If a different utilty (or general scoring)
function is desired, it is very simple to replace it.
par
subsectionDuration
labelutility:duration
par
For the utility of activity duration it seems to be widely believed
that the marginal utility of duration should be decreasing with longer
durations. We also think that the marginal utility of duration should
be nonnegative.
par
At first glance, this may seem to be not very intuitive because with
nonnegative marginal utility of duration for a single activity there
is nothing that limits its execution time. However, considering more
than one activity and a limited time budget, it can be seen that the
available time will be distributed in order to achieve a higher
overall utility. In the absence of other restrictions such as travel
times or opening times, the optimal time allocation for a given activity
pattern is reached if all activities have the same marginal utility of
duration.
par
We decided to use a logarithmic function as utility of duration:
beginequation
U_dur(t_dur) = beta_durcdot t_opt cdot
ln(fract_durt_0) .
endequation
Here,
are linear in
the time needed for that
activity. Despite the detailed discussion, it should be kept in mind
that the technology of using a GA is entirely independent from the
specific utility function. If a different utilty (or general scoring)
function is desired, it is very simple to replace it.
par
subsectionDuration
labelutility:duration
par
For the utility of activity duration it seems to be widely believed
that the marginal utility of duration should be decreasing with longer
durations. We also think that the marginal utility of duration should
be nonnegative.
par
At first glance, this may seem to be not very intuitive because with
nonnegative marginal utility of duration for a single activity there
is nothing that limits its execution time. However, considering more
than one activity and a limited time budget, it can be seen that the
available time will be distributed in order to achieve a higher
overall utility. In the absence of other restrictions such as travel
times or opening times, the optimal time allocation for a given activity
pattern is reached if all activities have the same marginal utility of
duration.
par
We decided to use a logarithmic function as utility of duration:
beginequation
U_dur(t_dur) = beta_durcdot t_opt cdot
ln(fract_durt_0) .
endequation
Here,  is the duration of the activity as it is actually
performed, and
is the duration of the activity as it is actually
performed, and 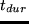 is the duration at which the utility starts to be
positive. This can be interpreted as minimal duration.
par
is the duration at which the utility starts to be
positive. This can be interpreted as minimal duration.
par
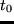 is the marginal utility of duration of the activity at its optimal duration
is the marginal utility of duration of the activity at its optimal duration
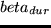 , as can be seen by taking the partial derivative:
beginequation
fracpartial Upartial t_dur(t_dur) =
fracbeta_durcdot t_optt_dur .
endequation
Setting
, as can be seen by taking the partial derivative:
beginequation
fracpartial Upartial t_dur(t_dur) =
fracbeta_durcdot t_optt_dur .
endequation
Setting
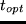 yields indeed
yields indeed 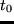 for the
marginal utility.
par
For unrestricted activities, one would assume that
for the
marginal utility.
par
For unrestricted activities, one would assume that
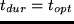 is the same for all activities that are
actually performed--otherwise the agent would just reallocate
durations in the direction of improvements. This allows to give
order-of-magnitude values for many of the free parameters in the
utility function.
par
For example, the marginal utility of duration around the operating point
should be similar to the utility of time
is the same for all activities that are
actually performed--otherwise the agent would just reallocate
durations in the direction of improvements. This allows to give
order-of-magnitude values for many of the free parameters in the
utility function.
par
For example, the marginal utility of duration around the operating point
should be similar to the utility of time 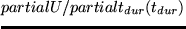 of the person that
we try to model. If one assumes that activity durations are usually
close to the optimal duration given by
of the person that
we try to model. If one assumes that activity durations are usually
close to the optimal duration given by 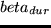 , then this means that
the parameter
, then this means that
the parameter 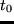 can be set to
can be set to
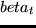 . We
will use
. We
will use
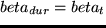 EUR
EUR 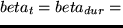 /h.
par
yy reference??
par
yy Ich habe hier keiner Referenz. Ich stütze mich auf deine
Aussagen. Dave -- Müsste man suchen, habe ich aber im Moment nicht.
Hoffentlich bei der nächsten Iteration des Papers. Kai
par
The marginal utility is independent of the minimal duration
/h.
par
yy reference??
par
yy Ich habe hier keiner Referenz. Ich stütze mich auf deine
Aussagen. Dave -- Müsste man suchen, habe ich aber im Moment nicht.
Hoffentlich bei der nächsten Iteration des Papers. Kai
par
The marginal utility is independent of the minimal duration 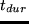 .
This means that for day plans that are not too tight the optimal
solution is almost independent of the
.
This means that for day plans that are not too tight the optimal
solution is almost independent of the 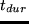 's. (If dayplans are
tight, the durations of some activities may drop below
's. (If dayplans are
tight, the durations of some activities may drop below 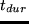 , in which
case this statement is no longer correct.) As a consequence, we can
use the parameters
, in which
case this statement is no longer correct.) As a consequence, we can
use the parameters 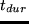 to ensure that the utilities of all
activities at their operating point have certain value. Based on the
utility of sleeping 8 hours with a
to ensure that the utilities of all
activities at their operating point have certain value. Based on the
utility of sleeping 8 hours with a 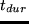 of 2 hours, we decided that
the utility of all activities at thier operating points should be
of 2 hours, we decided that
the utility of all activities at thier operating points should be
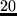 EUR
EUR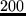 , where
, where 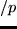 is a priority value. This yields the
following equation for the parameter
is a priority value. This yields the
following equation for the parameter 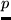 :
beginequationlabeleqn:t0
t_0
= t_optcdot e^-200EUR/(t_optcdot p cdot beta_t),
= t_optcdot e^-10mathrmh/(t_optcdot p),
endequation
A result of this is that even activities with a high priority can
still be dropped if they are very inconvenient. As we will see later,
this has sometimes inconvenient results, such as picking up a child
from kindergarten but never dropping it off. On the other hand, it is
certainly true that schedules can become so tight that even high
priority items are dropped, for example by asking someone else to help
out. For that reason, making high priority activities completely
obligatory is not plausible.
par
subsectionGeneralized travel costs
par
Traveling has a disutility that is linear in time, i.e.
:
beginequationlabeleqn:t0
t_0
= t_optcdot e^-200EUR/(t_optcdot p cdot beta_t),
= t_optcdot e^-10mathrmh/(t_optcdot p),
endequation
A result of this is that even activities with a high priority can
still be dropped if they are very inconvenient. As we will see later,
this has sometimes inconvenient results, such as picking up a child
from kindergarten but never dropping it off. On the other hand, it is
certainly true that schedules can become so tight that even high
priority items are dropped, for example by asking someone else to help
out. For that reason, making high priority activities completely
obligatory is not plausible.
par
subsectionGeneralized travel costs
par
Traveling has a disutility that is linear in time, i.e.
The disutility of traveling should be larger than disutility of waiting.
Otherwise, agents would prefer to stay on congested roads for a long time
instead of arriving too early at their destination.
We set
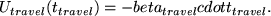 .
par
subsectionWaiting
par
Following the Vickrey model of departure time choice
citep[e.g.][]Arnott:etc:bottleneck, both waiting and arriving late
are penalized lineary. For waiting:
.
par
subsectionWaiting
par
Following the Vickrey model of departure time choice
citep[e.g.][]Arnott:etc:bottleneck, both waiting and arriving late
are penalized lineary. For waiting:
Here, 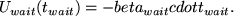 is the marginal disutility of waiting.
is the marginal disutility of waiting.
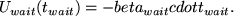 should be rather small; we will set it to
should be rather small; we will set it to  .
par
subsectionPenalty for late arrival
labelsec:penalty_late
par
For late arrival, this becomes
begindisplaymath
U_late.ar(t_start)=cases-beta_late.ar(t_start-t_latest.ar) & if
.
par
subsectionPenalty for late arrival
labelsec:penalty_late
par
For late arrival, this becomes
begindisplaymath
U_late.ar(t_start)=cases-beta_late.ar(t_start-t_latest.ar) & if
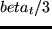 cr
0 & else. cr
enddisplaymath
Here,
cr
0 & else. cr
enddisplaymath
Here, 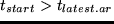 is the starting time of the activity,
is the starting time of the activity, 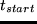 is the
latest possible starting time for the activity and
is the
latest possible starting time for the activity and
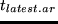 is a
parameter that quantifies the disutility of coming late.
is a
parameter that quantifies the disutility of coming late.
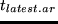 should be roughly as high as the utility of time
should be roughly as high as the utility of time
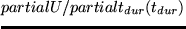 . We use
. We use
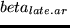 EUR/h.
par
subsectionPenalty for leaving too early
labelsec:penalty_early
par
We also have to introduce some penalty when an activity is ended too early.
We choose to make this linear in how much one leaves too early:
begindisplaymath
U_early.dp(t_end)=cases-beta_early.dp(t_earliest.dp-t_end) & if
EUR/h.
par
subsectionPenalty for leaving too early
labelsec:penalty_early
par
We also have to introduce some penalty when an activity is ended too early.
We choose to make this linear in how much one leaves too early:
begindisplaymath
U_early.dp(t_end)=cases-beta_early.dp(t_earliest.dp-t_end) & if
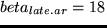 cr
0 & else. cr
enddisplaymath
Here,
cr
0 & else. cr
enddisplaymath
Here, 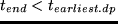 is the ending time of the activity,
is the ending time of the activity,
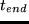 is the
earliest possible ending time for the activity and
is the
earliest possible ending time for the activity and
 is a
parameter that quantifies the disutility of leaving too early. For the parameter
is a
parameter that quantifies the disutility of leaving too early. For the parameter
 we used a value of
we used a value of  EUR/h.
par
subsectionOpening times and similar constraints
Many activities can only be carried out during certain times of the day.
For instance shopping can only be done when the stores are open.
The question is what utility we want to assign to activities which violate
these constraints.
par
One possibility would be to assign a very low utility to those
activities, e.g. minus infinity. This policy would be very efficient
in avoiding invalid day plans. But it would not make very much sense,
for the following reason: Assume that you have to compare two time
allocations for the activity ``shop''. In the first scenario you go
shopping at 7:59am and shop for two hours. In the second scenario you
go shopping at 8:00am and shop also for two hours. The shop opens at
8am. The first time allocation is invalid because you try to shop
while the shop is closed. So the utility of the first scenario would
be very low. The second scenario, however, has a very high utility.
With this policy, the minimal change of one minute in time allocation
would produce a huge change in utility which is certainly not
realistic. In reality, we would have waited one minute in front of
the shop. That means that one should set parameters such that both
utilities are almost the same.
par
pagebreak
Based on these reflections, we come up with the following constraint handling
policy:beginitemize
item At the beginning of the allocated time slot, we assume that the
agent travels from the location of the last activity to the location
of the new activity. The time spent for traveling yield a disutility
according to the section about travel costs.
item
From the moment of arrival at the activity location until the end of the
time slot, as much time as possible is spent actually performing the
activity.
item
If for some reason, for instance because of opening hours, it is not possible to
use all this time for performing the activity the remaining time is spent
waiting.
Waiting yields a negative utility according to the section above.
par
item Since we use a logarithmic function for the utility of duration,
it is possible that this utility becomes negative. If this is the
case, and if it is more efficient to spent the whole time waiting, the
activity is not executed at all. It may sound weird to travel to an
activity that is not executed. However, it is important to note that
we need to calculate meaningful utilities for no matter which day
plans the GA generates, because this is the material the GA works
with. Since traveling to an activity location without executing the
activity does not make sense, the GA will eventually find a better
solution, such as either completely dropping the activity, or
allocating sufficient time for it.
par
enditemize
par
subsectionTime of day dependence of utility
par
The utility of many activities depend on the time of day on which they
are executed. For example, many sports activities can even be carried
out only at daylight. The most complete model to take care of time of
day dependence would be to integrate a weighted marginal utility of
each activity over its whole duration. The weighting would then be
responsible for the time of day dependence.
par
Due to the complexity of this approach, and because there seems to be a lack of
information on how to model it in detail, we decided not to use any model for
time of day dependence.
We simply assume that there is no dependence. This means that
``leisure at 4am'' will result in the same utility as ``leisure at
8pm''.
par
Despite the bizarre example, we believe that--for most real world examples of
day plans--we do not sacrifice very much realism in our results.
There are many constraints that a day plan has to fulfill, leaving only very
little room for absurd day plans.
par
Note that for instance the ``beginning of work'' is already anchored because of
the late penalty, and shopping can only be done during opening times.
We may have to also anchor sleep since that is preferably done when it is dark.
par
subsectionSummary of parameters
par
The following is a listing of all parameters of our utility function and the
values that we used.
par
begintabularl r @
EUR/h.
par
subsectionOpening times and similar constraints
Many activities can only be carried out during certain times of the day.
For instance shopping can only be done when the stores are open.
The question is what utility we want to assign to activities which violate
these constraints.
par
One possibility would be to assign a very low utility to those
activities, e.g. minus infinity. This policy would be very efficient
in avoiding invalid day plans. But it would not make very much sense,
for the following reason: Assume that you have to compare two time
allocations for the activity ``shop''. In the first scenario you go
shopping at 7:59am and shop for two hours. In the second scenario you
go shopping at 8:00am and shop also for two hours. The shop opens at
8am. The first time allocation is invalid because you try to shop
while the shop is closed. So the utility of the first scenario would
be very low. The second scenario, however, has a very high utility.
With this policy, the minimal change of one minute in time allocation
would produce a huge change in utility which is certainly not
realistic. In reality, we would have waited one minute in front of
the shop. That means that one should set parameters such that both
utilities are almost the same.
par
pagebreak
Based on these reflections, we come up with the following constraint handling
policy:beginitemize
item At the beginning of the allocated time slot, we assume that the
agent travels from the location of the last activity to the location
of the new activity. The time spent for traveling yield a disutility
according to the section about travel costs.
item
From the moment of arrival at the activity location until the end of the
time slot, as much time as possible is spent actually performing the
activity.
item
If for some reason, for instance because of opening hours, it is not possible to
use all this time for performing the activity the remaining time is spent
waiting.
Waiting yields a negative utility according to the section above.
par
item Since we use a logarithmic function for the utility of duration,
it is possible that this utility becomes negative. If this is the
case, and if it is more efficient to spent the whole time waiting, the
activity is not executed at all. It may sound weird to travel to an
activity that is not executed. However, it is important to note that
we need to calculate meaningful utilities for no matter which day
plans the GA generates, because this is the material the GA works
with. Since traveling to an activity location without executing the
activity does not make sense, the GA will eventually find a better
solution, such as either completely dropping the activity, or
allocating sufficient time for it.
par
enditemize
par
subsectionTime of day dependence of utility
par
The utility of many activities depend on the time of day on which they
are executed. For example, many sports activities can even be carried
out only at daylight. The most complete model to take care of time of
day dependence would be to integrate a weighted marginal utility of
each activity over its whole duration. The weighting would then be
responsible for the time of day dependence.
par
Due to the complexity of this approach, and because there seems to be a lack of
information on how to model it in detail, we decided not to use any model for
time of day dependence.
We simply assume that there is no dependence. This means that
``leisure at 4am'' will result in the same utility as ``leisure at
8pm''.
par
Despite the bizarre example, we believe that--for most real world examples of
day plans--we do not sacrifice very much realism in our results.
There are many constraints that a day plan has to fulfill, leaving only very
little room for absurd day plans.
par
Note that for instance the ``beginning of work'' is already anchored because of
the late penalty, and shopping can only be done during opening times.
We may have to also anchor sleep since that is preferably done when it is dark.
par
subsectionSummary of parameters
par
The following is a listing of all parameters of our utility function and the
values that we used.
par
begintabularl r @ 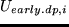 r @ l
Marginal utility of any activity:&
r @ l
Marginal utility of any activity:&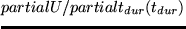 &
&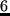 &EUR
&EUR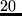 .
.
Marginal disutility of travel time:&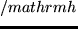 &
& &EUR
&EUR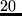 .
.
Marginal disutility of waiting:&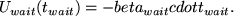 &
&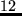 &EUR
&EUR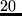 .
.
Marginal disutility of coming late:&
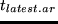 &
&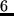 &EUR
&EUR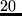 .
.
Marginal disutility of leaving too early:&
 &
&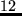 &EUR
&EUR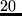 .
endtabular
par
subsectionPlots of utility landscape
par
In order to show some properties of the utility landscape, we exemplarily
analyze plots of some activity patterns.
Because of the limited number of displayable dimensions, our choice is
restricted to very short activity patterns with a maximum of four activities.
par
Now, if we would use full length day plans with such a limited number of activities,
the resulting day plans would be rather slack, and as a result of that, many of
the typical problems with activity planning would simply not arise.
par
Our way out of this problem is to use shorter time budgets for our example
activity plans.
In consequence, the plans that we are going to talk about here are no longer
complete day plans but rather partial plans.
However, since the calculation of the utility values is completely additive, having a look at partial
plans does make sense.
par
As a further simplification, we assume during our investigations that all
activities can be carried out at the same location.
By applying this simplification, we do not have to define a lot of
location related parameters.
However, the problems that can be observed in this simplified context
have the same complexity as with traveling enabled.
This is due to the fact that our travel times are independent of time of day and
because they are linear in the geometric distance of the locations.
par
We first show the typical utility landscape of an activity chain with four
activities emphhome, emphwork, emphleisure and emphhome. The
desired duration for emphwork, emphleisure and emphhome had
been set to 8, 2 and 4 hours respectively. There were no additional constraints
that had to be fulfilled except that the total length of the plan was fixed to
16 hours; i.e. there is a time surplus.
beginfigure
begincenter
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_hwlh_surplus.eps.gz
qquad
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_hwlh_surplus_contour.eps.gz
caption[utl home-work-leis-home]Utility of activity pattern
emphhome-work-leisure-home
.
endtabular
par
subsectionPlots of utility landscape
par
In order to show some properties of the utility landscape, we exemplarily
analyze plots of some activity patterns.
Because of the limited number of displayable dimensions, our choice is
restricted to very short activity patterns with a maximum of four activities.
par
Now, if we would use full length day plans with such a limited number of activities,
the resulting day plans would be rather slack, and as a result of that, many of
the typical problems with activity planning would simply not arise.
par
Our way out of this problem is to use shorter time budgets for our example
activity plans.
In consequence, the plans that we are going to talk about here are no longer
complete day plans but rather partial plans.
However, since the calculation of the utility values is completely additive, having a look at partial
plans does make sense.
par
As a further simplification, we assume during our investigations that all
activities can be carried out at the same location.
By applying this simplification, we do not have to define a lot of
location related parameters.
However, the problems that can be observed in this simplified context
have the same complexity as with traveling enabled.
This is due to the fact that our travel times are independent of time of day and
because they are linear in the geometric distance of the locations.
par
We first show the typical utility landscape of an activity chain with four
activities emphhome, emphwork, emphleisure and emphhome. The
desired duration for emphwork, emphleisure and emphhome had
been set to 8, 2 and 4 hours respectively. There were no additional constraints
that had to be fulfilled except that the total length of the plan was fixed to
16 hours; i.e. there is a time surplus.
beginfigure
begincenter
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_hwlh_surplus.eps.gz
qquad
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_hwlh_surplus_contour.eps.gz
caption[utl home-work-leis-home]Utility of activity pattern
emphhome-work-leisure-home
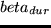 of work, leisure and home set to 8, 2 and 4 hours respectively
of work, leisure and home set to 8, 2 and 4 hours respectively
Total time budget of 16 hours, i.e. time surplus
labelfig:hwlh_surplus
endcenter
endfigure
par
The utility function of the two parameters emphduration of work and
emphduration of leisure has one clean global optimum. It should be
easy to find the global optimum of this activity pattern even with
standard optimization techniques. At the borders of the domain, there
exist small regions where the utility increases again.
This is due to the definition of the utility function which has a
cutoff at very short durations. For example, when the duration of
work becomes less than two hours, it becomes better to not work at
all, in which case the additional leisure time makes a positive
contribution.
par
Note in figure reffig:hwlh_surplus that the optimum is not at the three
``optimal'' durations 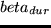 but at slightly longer durations. This is due to the fact that the desired
plan length of 16 hours is longer than the sum of the ``optimal''
durations which is 14 hours.
par
In order to show the effect of the time budget on the time allocation, we show
another plot of the same activity pattern but this time with a desired plan
length of 12 hours. See figure reffig:hwlh_tight.
par
beginfigure
begincenter
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_hwlh_tight.eps.gz
qquad
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_hwlh_tight_contour.eps.gz
caption[utl home-work-leis-home]Utility of activity pattern
emphhome-work-leisure-home
but at slightly longer durations. This is due to the fact that the desired
plan length of 16 hours is longer than the sum of the ``optimal''
durations which is 14 hours.
par
In order to show the effect of the time budget on the time allocation, we show
another plot of the same activity pattern but this time with a desired plan
length of 12 hours. See figure reffig:hwlh_tight.
par
beginfigure
begincenter
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_hwlh_tight.eps.gz
qquad
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_hwlh_tight_contour.eps.gz
caption[utl home-work-leis-home]Utility of activity pattern
emphhome-work-leisure-home
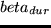 of work, leisure and home set to 8, 2 and 4 hours respectively
of work, leisure and home set to 8, 2 and 4 hours respectively
Total time budget of 12 hours, i.e. it is a tight plan
labelfig:hwlh_tight
endcenter
endfigure
par
Note that the optimum is shifted towards shorter times and the utility of the
optimum is roughly 100EUR lower.
par
note Show something more interesting: utl landscape that is time of day dependent
note opening times have large impact on utl
note Single activity, large complexity -> due to opening times
par
The utility landscape of activities with opening hours is much more complex. As
an example we show the utility of shopping in a store that is open during the
morning from 9 until 11 and in the afternoon from 14 until 17. Without opening
hours the landscape would be very smooth and completely independent of time of
day. emphWith the opening hours some interesting new properties can be
observed.
par
beginfigure
begincenter
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_shop.eps.gz
quad
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_shop_contour.eps.gz
caption[utl shop with opening times]Utility of activity emphshop. Shop open 9-11, 14-17. Note, in
contrast to the other plots of the utility landscape, in this plot
there is no constraint on the total length of the partial
plan. yy Ich finde, dass der 3d plot komisch aussieht. Vielleicht
mehr von der Seite gucken. Kai
labelfig:shop
endcenter
endfigure
par
note three locally optimal points->discuss
In figure reffig:shop we see that now there exist three local optima.
The global optimum corresponds to showing up in the shop at 9 in the morning
and staying there until 17 in the evening.
The lunch break is spent waiting.
The two local optima in the morning and the afternoon are much more meaningful.
The early local optimum corresponds to coming at 9am when the shop opens and
leaving the shop at 11am when it closes. The late local optimum corresponds to
coming at 14 when the shop opens and leaving at 17 when it closes.
The reason why the global optimum looks this way lies in the fact that our
marginal utility is always nonnegative. The effect of that is that shopping more
automatically yields more utility. However, it is important to note that the
additional utility is rather small, if shopping has already been performed for a
long time.
par
note combination with other activities yield even more complex structure
The structure of the fitness landscape becomes even more complex when we
consider an activity emphchain that includes a complex activity with opening hours.
Figure reffig:work-shop-work shows the utility of the activity
pattern emphwork-shop-work.
The desired durations for the activities were set to eight hours for the total
working duration and two hours for the shopping activity. The overall plan was
set to start at 8 and last until 17; i.e. the plan is tight.
beginfigure
begincenter
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_wsw.eps.gz
quad
includegraphics[width=0.4textwidth, height=0.4textwidth]gz/utl_wsw_contour.eps.gz
caption[utl work-shop-work]Utility of activity pattern
emphwork-shop-work. The shop is open 9-11 and 14-17.
Note, for the calculation of the utility of work only the total working duration
is regarded. That is, the sum of working duration before shopping and after
shopping is first calculated and then the utility for work is calcualted.
labelfig:work-shop-work
endcenter
endfigure
par
note two equvalent optima, shop morning, or shop afternoon
The utility for this activity pattern shows two equivalent global optima. They
correspond to go shopping in the morning for almost two hours and
to go shopping in the afternoon. The optimum in the afternoon is wider, because
the shop is open for three hours in the afternoon.
par
sectionTests and results
par
In this section, we want to show the general ability of our model to
generate complete day plans. For that purpose, we designed a simple
city. In our city there exist a number of different facilities
including apartments, working places, shops, kindergartens and
recreational areas. For each of these facilities, there exist three
different locations between which an agent can choose. The different
locations of the facilities are summarized in a map. See figure
reffig:map.
par
beginfigure
begincenter
includegraphics[width=0.8textwidth]map-fig.eps
captionMap of facilities
labelfig:map
endcenter
endfigure
par
For our tests we assume that travel times are simply proportional to
the geometric distance between two locations and that the travel speed
is constantly
 .
par
We want to test our algorithm for different kinds of agents with
different lists of activities that they would like to accomplish. For
this purpose, we defined three different scenarios. Each scenario is
defined by a set of activities that are available. The scenario
``full10'' is the one with the largest set and consist of ten
activities which are listed in figure reffigure:activities. The
other two scenarios use a subset of these activities.
par
beginfigure
begincenter
begintabularlllllll
hline
Name&priority &
.
par
We want to test our algorithm for different kinds of agents with
different lists of activities that they would like to accomplish. For
this purpose, we defined three different scenarios. Each scenario is
defined by a set of activities that are available. The scenario
``full10'' is the one with the largest set and consist of ten
activities which are listed in figure reffigure:activities. The
other two scenarios use a subset of these activities.
par
beginfigure
begincenter
begintabularlllllll
hline
Name&priority &
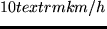 &
&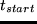
 &
&
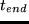
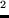 &
&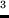
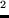 &Facility
&Facility
hline
sleep&1&8.0&25.0&29.0&6.0&home
early work&1&4.0&9.0&11.0&3.5&work
late work&1&4.0&14.0&15.0&3.5&work
breakfast&3&0.5&10.0& &0.25&home
lunch&2&1.25&14.0&12.0&0.75&work/home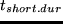
dinner&2&2.0&21.0&18.0&0.75&home
bring to kindergarten&1&0.25&9.0&8.5&0.25&kindergarten
fetch from kindergarten&1&0.25&16.0&15.5&0.25&kindergarten
shopping&3&2.0& & &0.5&shop
leisure&3&2.0& & &1.0&leisure
hline
endtabular
endcenter
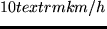 Note that
Note that 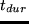 is derived from the priority and
is derived from the priority and 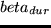 .
See section refutility:duration and equation (refeqn:t0).
.
See section refutility:duration and equation (refeqn:t0).
 Latest starting time. If the activity starts later a penalty is applied.
See section refsec:penalty_late
Latest starting time. If the activity starts later a penalty is applied.
See section refsec:penalty_late
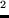 Both,
Both,
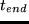 and
and 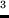 address the problem of not
executing an activity enough long. If the activity is ended before
address the problem of not
executing an activity enough long. If the activity is ended before
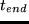 a penalty applies. The same penalty applies if the duration of
the activity is shorter than
a penalty applies. The same penalty applies if the duration of
the activity is shorter than 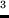 . See
section refsec:penalty_early
. See
section refsec:penalty_early
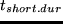 Depending on the scenario, the facility of the activity ``lunch'' was
either work or home. See description of the scenarios.
captionActivities of our test case
labelfigure:activities
endfigure
par
beginfigure
begincenter
begintabularlc
hline
Facility Name & Opening Times
Depending on the scenario, the facility of the activity ``lunch'' was
either work or home. See description of the scenarios.
captionActivities of our test case
labelfigure:activities
endfigure
par
beginfigure
begincenter
begintabularlc
hline
Facility Name & Opening Times
hline
Home & 00:00-24:00
Work & 06:00-20:00
Kindergarten & 8:30-9:00 15:30-16:00
Shop & 09:00-19:00
Leisure & 14:00-24:00
hline
endtabular
endcenter
captionOpening times of the facilities.
An activity can only be carried out when the required facility is open.
Note facility ``Kindergarten'' has two opening times. The first one defines when
children can be dropped off and the second when they can be picked up.
labelfigure:opening-times
endfigure
par
All facilities needed by the activities except for the facility ``home'' are not
open during the whole day.
The opening times used for our investigations are summarized in
figure reffigure:opening-times.
par
The three scenarios are defined as follows:
beginitemize
item As mentioned above, the ``full10'' scenario defines a scenario with set of
ten activities.
This scenario consists of the activities
``sleep'', ``breakfast'', ``lunch'', ``dinner'',
``early work'', ``late work'',
``bring children to kindergarten'', ``fetch children from kindergarten'',
``shop'', and ``leisure''.
The purpose of this scenario is to show the performance of our algorithm if
there are very many activities to perform.
item In the ``houseman'' scenario, the agent has only eight of the ten
activities of the ``full10'' scenario to choose from, leaving out both work
activities.
That is, the remaining activities are:
``sleep'', ``breakfast'', ``lunch'', ``dinner'',
``bring children to kindergarten'', ``fetch children from kindergarten'',
``shop'' and ``leisure''.
Since in this scenario the agent does not have a work location, we
changed the facility for eating lunch from ``work'' to ``home''.
This scenario simulates a rather dense day plan of a non working person.
item samepage
In the ``pensioner'' scenario, the set of activities consists only of 5
activities; these are ``sleep'', ``lunch'', ``dinner'', ``shopping''
and ``leisure''.
As in the ``houseman'' scenario, the facility for having lunch was changed to
``home''.
With this scenario we want to show how our model deals with day plans with a
large freedom in time allocation.
enditemize
par
We do two separate investigations for each scenario. In the first investigation
we run the algorithm for a long time in order to rate the quality of the best
solution that the algorithm possibly produces.
In the second investigation we want to rate if the algorithm is
capable of finding usable day plans within a limited time, therefore we run the
program for a short time.
This second question is especially important if we want to generate day plans a
large number of agents.
par
For the quality investigation we run the algorithm for 10,000,000 generations
with a GA-population size of 300. The execution takes between 140 and 230
seconds on a 2.4GHz Pentium 4 Laptop.
For the usability and speed investigation we change the parameters in order to
achieve a higher convergence speed taking into account that we sacrifice some
stability for that reason. The GA-population size is reduced to 50 and the
number of generations is limited to 200,000. Here, the execution takes between
3 and 5 seconds.
par
note convergence graph for quality of full10
par
beginfigure
begincenter
includegraphics[width=0.8textwidth]convergence_full10_long-gpl.eps
captionConvergence graph for ``full10'' scenario. The test was run for 10 mio iterations
in order to get the best possible quality of the resulting day plan.
The graph shows the maximal and average utility of the population of a typical
long run.
labelfig:conv-long
endcenter
endfigure
par
note convergence graph for usability and speed of full 10
par
beginfigure
begincenter
includegraphics[width=0.8textwidth]convergence_full10_short-gpl.eps
captionConvergence graph for ``full10'' scenario. The tests were run for only 200,000
iterations to test the performance of the algorithm if there is only limited time
for finding a good day plan. The graph shows the maximum utility of the
population for the best and the worst short run.
labelfig:conv-short
endcenter
endfigure
par
note time allocation and location choice figure for full10 (quality)
The quality test for the ``full10'' scenario was run with 5 different
initializations.
At the end of each run, the day plan with the highest utility value was always
identical in terms of generated pattern and location selection.
Only the time allocations differed, but the differences were within very few
minutes.
In figure reffig:conv-long we show a typical convergence graph for the
quality tests.
The best day plan found for the ``full10'' scenario in the quality test is shown
in figure reffigure:full10_long.
Note that the children are not dropped off at home before continuing with the day
plan; especially ``leisure'' is performed together with the children.
This can be observed in almost all generated day plans.
The reason for this shortcoming is the absence of a constraint that would force
the agents to drop children off before starting with the next activity.
The way we have modeled the utility function it is clearly preferable to take
the children along because this minimizes traveling distance.
par
beginfigure
begincenter
includegraphics[width=0.54textwidth]map_full10_long-fig.eps
par
bigskip
par
begintabularllll
hline
Activity Name & Travel Time & Execution Time & Location
hline
Breakfast& & 06:56-07:26 & home 0
Bring children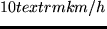 & 07:26-08:30 & 08:30-08:40 & kiga
& 07:26-08:30 & 08:30-08:40 & kiga 2
2
Early work & 08:40-08:46 & 08:46-11:52 & work 2
Lunch & & 11:52-12:40 & work 2
Late work & & 12:40-15:40 & work 2
Fetch children & 15:40-15:46 & 15:46-16:00 & kiga
& 15:40-15:46 & 15:46-16:00 & kiga 2
2
Shop & 16:01-16:43 & 16:43-18:26 & shop 0
Leisure & 18:26-18:48 & 18:48-20:27 & leisure 1
Dinner & 20:27-21:03 & 21:03-23:02 & home 0
Sleep & & 23:02-06:56 & home 0
hline
endtabular
endcenter
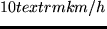 Bring children to the kindergarten.
Bring children to the kindergarten.
 Fetch children from the kindergarten.
Fetch children from the kindergarten.
 Kindergarten
captionBest day plan for the ``full10'' scenario after 10 mio iterations.
The total utility is 1284.93EUR. The map graphically summarizes the day plan.
labelfigure:full10_long
endfigure
par
note time allocation and location choice figure for full10 (usability)
par
In the five short runs for investigation of speed and usability for the scenario
``full10'' three times a solution
was found that is identical to the one shown in figure reffigure:full10_long
in terms of generated pattern and selected
locations. Only the time allocations were not as sophisticated. The total
utility varied between 1277.54 and 1278.84EUR.
In the two remaining runs, two different solutions were found. The solution
shown in figure reffigure:full10_short_sp1
differs only in terms of location selection
and time allocation while the solution shown in
figure reffigure:full10_short_sp2
differs also in the generated pattern.
Note that in this day plan the activity ``bring children to kindergarten'' is
left out.
In figure reffig:conv-short we compare the convergence of the best and the
worst short run.
par
beginfigure
begincenter
includegraphics[width=0.54textwidth]map_full10_short_sp1-fig.eps
par
bigskip
par
begintabularllll
hline
Activity Name & Travel Time & Execution Time & Location
Kindergarten
captionBest day plan for the ``full10'' scenario after 10 mio iterations.
The total utility is 1284.93EUR. The map graphically summarizes the day plan.
labelfigure:full10_long
endfigure
par
note time allocation and location choice figure for full10 (usability)
par
In the five short runs for investigation of speed and usability for the scenario
``full10'' three times a solution
was found that is identical to the one shown in figure reffigure:full10_long
in terms of generated pattern and selected
locations. Only the time allocations were not as sophisticated. The total
utility varied between 1277.54 and 1278.84EUR.
In the two remaining runs, two different solutions were found. The solution
shown in figure reffigure:full10_short_sp1
differs only in terms of location selection
and time allocation while the solution shown in
figure reffigure:full10_short_sp2
differs also in the generated pattern.
Note that in this day plan the activity ``bring children to kindergarten'' is
left out.
In figure reffig:conv-short we compare the convergence of the best and the
worst short run.
par
beginfigure
begincenter
includegraphics[width=0.54textwidth]map_full10_short_sp1-fig.eps
par
bigskip
par
begintabularllll
hline
Activity Name & Travel Time & Execution Time & Location
hline
Breakfast& & 07:27-07:56 & home 0
Bring children & 07:56-08:30 & 08:30-08:42 & textbfkiga 1
Early work & 08:42-09:03 & 09:03-11:54 & textbfwork 0
Lunch & & 11:54-12:49 & textbfwork 0
Late work & & 11:54-12:49 & textbfwork 0
Fetch children& 15:18-15:39 & 15:39-15:57 & textbfkiga 1
Shop & 15:57-16:33 & 16:33-18:13 & shop 0
Leisure & 18:13-18:35 & 18:35-20:26 & leisure 1
Dinner & 20:26-21:02 & 21:02-23:30 & home 0
Sleep & & 23:30-07:27 & home 0
hline
endtabular
endcenter
captionfirst alternative day plan for the ``full10'' scenario after 200,000 iterations.
The total utility is 1276.46EUR.
labelfigure:full10_short_sp1
endfigure
par
beginfigure
begincenter
includegraphics[width=0.54textwidth]map_full10_short_sp2-fig.eps
par
bigskip
par
begintabularllll
hline
Activity Name & Travel Time & Execution Time & Location
hline
Breakfast& & 06:14-06:46 & home 0
Early work& 06:46-06:59 & 06:59-10:56 & work 1
Lunch& & 10:56-11:59 & work 1
Late work& & 11:59-15:04 & work 1
Fetch children& 15:04-15:51 & 15:51-16:00 & kiga 1
Shop& 16:00-16:37 & 16:37-18:26 & shop 0
Leisure& 18:26-18:47 & 18:47-20:27 & leisure 1
Dinner& 20:27-21:03 & 21:03-23:06 & home 0
Sleep& & 23:06-06:14 & home 0
hline
endtabular
endcenter
captionSecond alternative day plan for the ``full10'' scenario after 200,000 iterations.
The total utility is 1107.89EUR. Note, the activity ``bring children to
kindergarten'' is left out.
labelfigure:full10_short_sp2
endfigure
par
note time allocation and location choice figure for pensioner (quality)
note time allocation and location choice figure for pensioner (usability)
par
In all runs for the ``pensioner'' scenario (five long runs and five short
runs) the same day plan was found with
respect to the generated activity pattern and the selected locations. The time
allocations to the different activities was also very similar. The similarity of
the day plans can also be seen when looking at the total utility which was
always between 638.483 and 638.514EUR--a very narrow interval. The only
difference between the plans was their starting time which varied in the range
from 10:33am to 11:45am. This is due to the lack of constraints for the
activities. That is, it does not matter at which time inside the range the day
plan starts. In figure reffigure:pensioner
we show the best day plan found. It starts at 11:45am.
par
beginfigure
begincenter
includegraphics[width=0.54textwidth]map_pensioner-fig.eps
par
bigskip
par
begintabularllll
hline
Activity Name & Travel Time & Execution Time & Location
hline
Lunch& & 11:45-13:36 & home 0
Shop& 13:36-13:57 & 13:57-16:54 & shop 0
Leisure& 16:54-17:15 & 17:15-20:14 & leisure 1
Dinner& 20:14-20:50 & 20:50-23:47 & home 0
Sleep& & 23:47-11:45 & home 0
hline
endtabular
endcenter
captionbest day plan found for ``pensioner'' scenario. The total utility is 638.514EUR.
labelfigure:pensioner
endfigure
par
It seems that our algorithm has no problems to find a good solution for
the ``pensioner'' scenario. In order to test this assumption we show the
convergence graph of one of the usability runs in
figure reffig:conv-pensioner-short.
One can see that the algorithm converges already very early.
In fact, a solution identical to the one shown in
figure reffigure:pensioner in terms of generated pattern
and selected locations is already found after 30,000 generations--which is
only 15% of total number of generations.
par
beginfigure
begincenter
includegraphics[width=0.8textwidth]convergence_pensioner_short-gpl.eps
caption
Convergence graph for ``pensioner'' scenario for a typical short run. In this
test, the goal was to find a good day plan within limited time.
labelfig:conv-pensioner-short
endcenter
endfigure
par
note time allocation and location choice figure for houseman (quality)
note time allocation and location choice figure for houseman (usability)
par
In all five long runs for the ``houseman'' scenario and in four of the five
short runs the same day plan was found with respect to the generated activity
pattern and the selected locations.
The time allocations were also very similar, they all lay within ten minutes.
The resulting utilities vary between 1040.51 and 1043.04EUR.
We show the best day plan found in figure reffigure:houseman-best.
par
beginfigure
begincenter
includegraphics[width=0.54textwidth]map_houseman_best-fig.eps
par
bigskip
par
begintabularllll
hline
Activity Name & Travel Time & Execution Time & Location
hline
Bring children & 08:08-08:42 & 08:42-08:59 & kiga 1
Breakfast& 08:59-09:33 & 09:33-10:17 & home 0
Lunch & & 10:17-12:02 & home 0
Shop & 12:02-12:23 & 12:23-14:58 & shop 0
Fetch children& 14:58-15:35 & 15:35-15:52 & kiga 1
Leisure & 15:52-16:19 & 16:19-18:51 & leisure 1
Dinner & 18:51-19:27 & 19:27-22:02 & home 0
Sleep & & 22:02-08:08 & home 0
hline
endtabular
endcenter
captionbest day plan found for the ``houseman'' scenario.
The total utility is 1043.04EUR.
Note that the agent fetches the children and performs activity ``leisure'' with
them. The reason why it does not drop them off at home before is that there is
no constraint forcing it to do so and the presented day plan minimizes travel
time.
labelfigure:houseman-best
endfigure
par
The day plan found in the remaining short run is topologically different from
the other day plans. It leaves out the activity ``leisure''.
See figure reffigure:houseman-second.
par
beginfigure
begincenter
includegraphics[width=0.54textwidth]map_houseman_second-fig.eps
par
bigskip
par
begintabularllll
hline
Activity Name & Travel Time & Execution Time & Location
hline
Breakfast& & 07:13-08:05 & home 1
Bring children & 08:05-08:30 & 08:30-09:00 & kiga 1
Shop & 09:06-09:52 & 09:52-12:36 & shop 2
Lunch & 12:36-12:58 & 12:58-15:03 & home 1
Fetch children& 15:03-15:28 & 15:30-15:58 & kiga 1
Dinner & 15:58-16:23 & 16:23-19:20 & home 1
Sleep & & 22:02-08:08 & home 1
hline
endtabular
endcenter
captionsecond day plan found for the ``houseman'' scenario.
The total utility is 1019.66EUR.
labelfigure:houseman-second
endfigure
par
note Summary of the results
par
The resulting day plans for all three scenarios are very convincing throughout.
All aspects of activity planning--activity pattern generation, location
selection and time allocation--are taken care of very well.
The convergence of the genetic algorithm seems to be very stable, as for each
scenario at the end of almost all test runs the same good solution is found.
It seems, that our tests have not yet pushed our algorithm to its limits, it
would be interesting to see how it performs on generating complete
week plans.
par
sectionFurther work
One interesting aspect of activity planning is to generate activity plans for
households instead of generating them for single agents.
This problem is more complex than simply generating individual day plans for each
of the occupants of a household since the all-day activity plans of different
occupants depend on each other.
For instance, only one of the agents living in a household has to go shopping.
par
The present model that we use for estimation of travel times between different
locations is not very realistic.
We are planning to include travel times from a simulation in order to increase
realism.
With time dependent travel times we hope that phenomena like congestion
avoidance within the day plans will emerge.
par
We would like to use the presented method to generate the individual day plans
for the agents of traffic simulations with up to 10 mio agents.
From that point of view it is clear that we have to make our algorithm much
faster.
One way to do that would be to use only a preselected set of activity patterns
instead, i.e. limiting the search space, or to generate simultaneously the
day plan for multiple similar agents.
par
sectionSummary
par
A genetic algorithm (GA) was presented that constructs all-day activity
plans. It uses as input a set of possible activities, and a utility
function to score activity schedules. The GA attempts to construct
good solutions which maximize the utility function. It does that by
maintaining a emphpopulation of solution instances, which are
mutated, and which, importantly, breed new solutions by crossover.
Crossover means that two solution instances are selected, and part of
the new solution comes from one parent, and the other part from the
other parent.
par
The algorithm is then run on several examples. It is shown that the
algorithm generates plausible solutions both for crowded and for
relaxed activity sets, and that it can do so even when the computation
time is restricted.
par
The most important aspect of this work is that arbitrary utility
functions can be used. A GA does not guarantee optimal solutions, but
it will nearly always generate plausible solutions. Given that humans
do no better, this may be sufficient for most if not all travel
forecasting purposes.
par
section*Acknowledgments
par
Kay Axhausen helped us along the way with numerous pointers to
actually evaluate all-day utility functions. Nevertheless, the
responsibility for our choices remains with us.
par
bibliographystyleiatbr
par
bibliographyprojects,ref,kai,xref
par
enddocument



Nächste Seite: Über dieses Dokument ...
2003-07-17