

Next: Bibliography
Up: Dynamic Traffic Assignment on
Previous: Acknowledgments
In this appendix, we explain the methodology for our performance
predictions. We start by assuming that the time for one time step has
contributions from computation and from communication. If they do not
overlap, as is reasonable to assume for coupled workstations, we have
Time for computation is assumed to follow
Here, T1 is the time of the same code on one CPU (assuming a
problem size that is rescaled to available memory); p is the number
of CPUs;
foverhead includes overhead effects (for example, split
edges need to be administered by both CPUs);
fdomainsincludes the effect of unequal domain sizes discussed in
Sec. 5.2.
Time for communication is assumed to follow
nneighb is the number of neighboring ``tiles'' each CPU talks to;
for the bisection algorithm this number approaches four. tlat is
the latency (or start-up time) of each message. Next come two terms
that describe bandwidth effects. If is necessary to use two terms
because bandwidth is limited by two factors:
- First, it is limited by the connection of the computer to the
network. For example, with our Sparc 5s we could never obtain more
than 30-40 Mbit/sec, although our FDDI network had a bandwidth of
more than 100 Mbit/sec.
- Thus, only when three or more pairs of machines start talking to
each other, we start seeing the network bandwidth saturation
effects.
One way to model these effects are the above two terms.
Nsplitedges is the number of split edges after the domain
decomposition; it is the number shown in Fig. 7.
Remember that
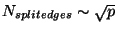 .
tedge is the time
that the network connection of the CPU needs for one additional split
edge.
.
tedge is the time
that the network connection of the CPU needs for one additional split
edge.
C/Csat models the effect of network saturation. It depends on
the network topology:
- For example, for a bus topology (e.g. a local area network, or
the Sparc Enterprise computers), C is just the amount of overall
communication, that is (neglecting message headers)
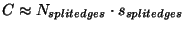 ,
where
ssplitedges is the
amount of data for each split edge. Csat is simply the
bandwidth of the communication medium, for example
100 Mbit/sec for a 100-Mbit-Ethernet.
,
where
ssplitedges is the
amount of data for each split edge. Csat is simply the
bandwidth of the communication medium, for example
100 Mbit/sec for a 100-Mbit-Ethernet.
- For a two-dimensional grid topology, C/Csat is negligible.
This can be seen as follows: Given a problem size, then for each
additional CPU the amount of information C exchanged between two
CPUs actually goes down, while the bandwidth between these two CPUs,
Csat remains the same.
In consequence, the combined time for one time step is
which (for
foverhead and
fdomains small enough) scales as
For bus topologies,
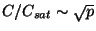 eventually becomes the
dominating term, explaining why the real time ratio, which goes as
eventually becomes the
dominating term, explaining why the real time ratio, which goes as
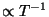 ,
eventually goes down in Fig. 12.
For 2-d topologies, C/Csat is negligible, and it is in practice
fdomains, the domain decomposition imbalance, that makes using
more than about 1000 CPUs inefficient.
,
eventually goes down in Fig. 12.
For 2-d topologies, C/Csat is negligible, and it is in practice
fdomains, the domain decomposition imbalance, that makes using
more than about 1000 CPUs inefficient.
This is the analysis which is behind Fig. 12.
Constants such as tedge or tlat were obtained from
systematic measurements of simplified situations.
See [] for more information.


Next: Bibliography
Up: Dynamic Traffic Assignment on
Previous: Acknowledgments
Kai Nagel
1999-12-12