Nurhan Cetin1, Kai Nagel2
Dept. of Computer Science, ETH Zürich, 8092 Zürich,
Switzerland
Keywords: Traffic Simulation, Queue Model, Parallel Programming, MPI
Queueing theory is the study of systems of queues where items arrive to the queues for service, wait in the queues for a while, receive service from one or more servers, and leave. Queues, i.e, waiting lines, form because resources are limited. Queueing theory deals with problems which involve waiting lines, i.e, it handles the problems of congestion.
Queueing theory studies the issues such as the rate of arrivals at the queue, the average waiting time until being served, the average queue length, etc., by knowing arrival rates and service rates. Queues in a system have a certain service rate. If the arrival rate of the items is greater than the service rate, queues are created to keep the excessive arrivals.
In this paper, we model traffic based on an extended version of queueing theory. We will use the term ``Queue Model'' instead of the term ``Queueing Theory'' in order to stress those extensions. Our aim is to simulate the links as queues and to make the intersection logic realistic.
In queueing theory, it is usual to define queues of infinite length. If the capacity of a queue is finite, queueing theory defines the system loss as follows: If a new item arrives to a queue which does not have any empty space, then the item leaves without being served (the item is called ``lost''). In our case, instead of losing the item, we refuse to accept it, which means that it does not get served at the upstream server even if the server has free capacity. Since this behavior can cause deadlocks (loops of completely congested queues), we remove vehicles from the simulation if they have not moved for a certain amount of time. Our goal, however, is to have a simulation which does not lose any items.
The paper is organized as follows: Implementation of queue model is explained in section 2. Section 3 gives an introduction to parallel programming. Parallel implementation of the queue model is given in Section 4. Section 5 discusses the simulation results.
In our model, the streets (links) are represented by finite queues. The dynamics of the queue model described and implemented here focus on two main reasons of a congestion. The first of these reasons is defined by not allowing more vehicles to leave a link per time step than the number of vehicles that are allowed to leave according to the link's capacity. This is the capacity constraint. The second one is that links can only store a certain number of vehicles, which we call the storage constraint. The storage constraint causes queue spill-back, and it reduces the number of incoming vehicles to the link once a link is full.
In consequence, each link is represented by a queue with a free flow
velocity ![]() , a length
, a length ![]() , a capacity
, a capacity ![]() and a number of lanes
and a number of lanes
![]() . Free flow velocity is the velocity of a car when the
traffic density is very low such that a car can go through that
particular link as fast as possible. Free flow travel time is
calculated by
. Free flow velocity is the velocity of a car when the
traffic density is very low such that a car can go through that
particular link as fast as possible. Free flow travel time is
calculated by
![]() .
.
The storage constraint of a link is calculated as
![]() , where
, where ![]() is the space a
single vehicle in the average occupies in a jam, which is the inverse
of the jam density. We use
is the space a
single vehicle in the average occupies in a jam, which is the inverse
of the jam density. We use
![]() .
The flow capacity, on the other hand, is given by the input files.
.
The flow capacity, on the other hand, is given by the input files.
As mentioned above, vehicles in the simulation can get stuck if congested links form a closed loop, and the vehicles at the downstream end of each of these links want to move into the next of these full links. In order to prevent this gridlock, any vehicle at the beginning of a queue that has not moved for over 300 simulation time steps (seconds) is removed from the simulation.
The queue model is implemented using the algorithm shown in
Alg. 1. The algorithm given there is based on the
algorithm described in [1,6] but with
a modified intersection dynamics. In those references, the
intersection logic essentially is:

The three conditions mean the following:
The problem with this algorithm is that links are always selected in the same sequence, thus giving some links a higher priority than others under congested conditions. Note that the ``winning'' link is not the link which is earliest in the sequence, but the link which is first after when traffic on the destination link has moved.
Simple randomization of the link sequence is only a partial remedy
since what one truly wants is to give links with a higher capacity
also a higher priority. In consequence, we have modified the
algorithm so that links are prioritized randomly according to
capacity. That is, links with high capacity are more often first than
links with low capacity. At the same time, we have moved the
algorithm from link-oriented to intersection-oriented (that is, the
loop now goes over all intersections, which then look at all incoming
links), and we have separated the capacity constraint from the
intersection logic. The last was done by introducing a separate
buffer at the end of the link, which is of size
![]() , i.e. the first integer number being larger or equal than the
link capacity (in vehicles per time step). Vehicles are then moved
from the link into the buffer according to the capacity constraint
and only if there is space in the buffer; once in the buffer,
vehicles can be moved across intersections without looking at the
capacity constraints.
, i.e. the first integer number being larger or equal than the
link capacity (in vehicles per time step). Vehicles are then moved
from the link into the buffer according to the capacity constraint
and only if there is space in the buffer; once in the buffer,
vehicles can be moved across intersections without looking at the
capacity constraints.
The above details are given in algorithmic form in Alg. 1. In addition and in preparation for parallel computing, we have made the dynamics of the algorithm completely parallel. What this means is that, if traffic is moved out of a full link, the new empty space will not become available until the next time step - at which time it will be shared between the incoming links according to the method described above. This has the advantage that all information which is necessary for the computation of a time step is available locally at each intersection before the time step starts - and in consequence there is no information exchange between intersections during the computation of the time step.
The idea behind parallel computing is that a task can be achieved faster if it is divided into a set of subtasks each of which is assigned to a different processor. The aim is to speed up the computation as a whole.
A possible parallel computation environment is for example a cluster of standard Pentium computers, coupled via standard 100 Mbit Ethernet LAN. Each computer would then get a subtask as described above.
In order to generate a parallel program, one must think about (i) how to partition the tasks into subtasks, (ii) how to provide the data exchange between the subtasks. One possibility of partitioning is to decompose the task so that each subtask can run the same program on a smaller portion of data independent of the other subtasks. When a subtasks needs information/data from another subtask, then communication is required.
As an example, a traffic simulation might take a long time to run if the underlying network is large and the number of vehicles is high. If one cares about fast computation time, then parallel computing is a solution since it solves the problem cost-effectively by aggregating the power and memory of many computers. What needs to be done is to partition the street network and to distribute the vehicles according to the partitioning information. If a vehicle needs to move into a link which is on an another partition, then a communication between these two partitions takes place.
Partitioning of a domain can be done in several ways. Finding the best way of doing a decomposition depends on what is to be decomposed. In our traffic simulation, we need to divide the network (of the streets and the intersections) into a number of subnetworks. In order to achieve this, we use a software package called METIS [2] which is based on multilevel graph partitioning. After the partitioning is done, each processor is assigned to a subpart.
With respect to communication, there are in general two main approaches to inter-processor communication. One of them is called message passing between processors; its alternative is to use shared-address space where variables are kept in a common pool where they are globally available to all processors. Each paradigm has its own advantages and disadvantages.
In the shared-address space approach, all variables are globally accessible by all processors. Despite multiple processors operating independently, they share the same memory resources. Accessing the memory should be provided in a mutually exclusive fashion since accesses to the same variable at the same time by multiple processors might lead to inconsistent data. Shared-address space approach makes it simpler for the user to achieve parallelism but since the memory bandwidth is limited, severe bottlenecks are unavoidable with the increasing number of processors, or alternatively such shared memory parallel computers become very expensive. Also, the user is responsible for providing the synchronization constructs in order to provide concurrent accesses.
In the message passing approach, there are independent cooperating processors. Each processor has a private local memory in order to keep the variables and data, and thus can access local data very rapidly. If an exchange of the information is needed between the processors, the processors communicate and synchronize by passing messages which are simple send and receive instructions. Message passing can be imagined similar to sending a letter. The following phases happen during a message passing operation.
The communication among the processors can be achieved by using a message passing library which provides the functions to send and receive data. There are several libraries such as MPI [3] (Message Passing Interface) or PVM [5] (Parallel Virtual Machine) for this purpose. Both PVM and MPI are software packages/libraries that allow heterogeneous PCs interconnected by a network to exchange data. They both define an interface for the different programming languages such as C/C++ or Fortran. For the purposes of parallel traffic simulation, the differences between PVM and MPI are negligible; we use MPI since it has slightly more focus on computational performance.
The size of input usually determines the performance of a sequential algorithm (or program) evaluated in terms of execution time. However, this is not the case for the parallel programs. When evaluating parallel programs, besides the input size, the computer architecture and also the number of the processors must be taken into consideration.
There are various metrics to evaluate the performance of a parallel program. Execution time, Speedup and Efficiency are the most common metrics to measure the performance of a parallel program. We will discuss these metrics in the following subsections.
The execution time of a parallel program is defined as the total time
elapsed from the time the first processor starts execution to the time
the last processor completes the execution. During execution, a
processor is either computing or communicating. Therefore,
For traffic simulation, the time required for the computation, namely,
![]() can be calculated roughly in terms of the serial execution
time (run time of the algorithm on a single CPU) divided by the number
of processors. Thus,
can be calculated roughly in terms of the serial execution
time (run time of the algorithm on a single CPU) divided by the number
of processors. Thus,
As mentioned above, time for communication typically has two
contributions: Latency and bandwidth. Latency is the time necessary
to initiate the communication i.e, the message size has no effect
here. Bandwidth describes the number of bytes that can be exchanged
per second. So the time for one message is
Maybe the most useful metric in measuring performance of a parallel
program is how much performance gain is achieved by the program.
Speedup achieved by a parallel algorithm is defined as the ratio of
the time required by the best sequential algorithm to solve a problem,
![]() , to the time required by parallel algorithm using
, to the time required by parallel algorithm using ![]() processors to solve the same problem,
processors to solve the same problem, ![]() :
:
Speedup is limited by a couple of factors. First, the software overhead appears in the parallel implementation since the parallel functionality requires additional lines of code. Second, speedup is generally limited by the speed of the slowest node or processor. Thus, we need to make sure that each node performs the same amount of work. i.e. the system is load balanced. Third, if the communication and computation cannot be overlapped, then the communication will reduce the speed of the overall application.
A final limitation of the speedup is known as Amdahl's Law - Serial
Fraction. This states that the speedup of a parallel algorithm is
effectively limited by the number of operations which must be
performed sequentially. Thus, let us define, for a sequential program,
![]() as the amount of the time spent by one processor on sequential
parts of the program and
as the amount of the time spent by one processor on sequential
parts of the program and ![]() as the amount of the time spent by
one processor on parts of the program that can be parallelized. Then,
we can formulate the serial run-time as
as the amount of the time spent by
one processor on parts of the program that can be parallelized. Then,
we can formulate the serial run-time as
![]() and
the parallel run-time as
and
the parallel run-time as
![]() .
.
Therefore, the serial fraction ![]() will be
will be


As an illustration, let us say, we have a program of which 80% can be
done in parallel and 20% must be done sequentially. Then even for ![]() , we have
, we have
![]() , meaning that even with an
infinite number of processors we are no more than 5 times faster than
we were with a single processor.
, meaning that even with an
infinite number of processors we are no more than 5 times faster than
we were with a single processor.
An ideal system with ![]() processors might have a speedup up to
processors might have a speedup up to
![]() . However, this is not the case in practice since, as pointed out
above, some parts of the program cannot be parallelized
efficiently. Also, processors will spend time on communication.
Efficiency is defined as
. However, this is not the case in practice since, as pointed out
above, some parts of the program cannot be parallelized
efficiently. Also, processors will spend time on communication.
Efficiency is defined as
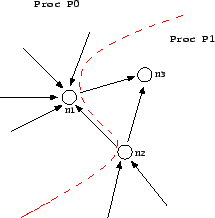
The decomposition at the boundaries of the subnetworks in our
simulation is shown in Figure 2. Each node
has
outgoing and incoming links. As shown in Figure ![]() , the nodes at the boundaries are divided in a way that
the nodes and the incoming links of those nodes are on the same
processor.
, the nodes at the boundaries are divided in a way that
the nodes and the incoming links of those nodes are on the same
processor.
|
Whenever a vehicle is at the boundary of a processor and needs to go to a link which is located on another processor, the vehicle is sent to that other processor by using message passing. The neighbor processor receives the vehicle and inserts it into the appropriate link.
There is actually another parallel communication step which is necessary before the intersection dynamics is run. In that communication step, each link sends its number of empty spaces to its from-node, i.e. the node where it is an outgoing link. If link and node are on the same processor, this is a simple data copy operation; if they are on different processors, then this involves a send and receive. The resulting parallel algorithm is given as Alg. 2.
In order to run our parallel application, we run it on a cluster of 32 Pentium PCs connected by 100 Mbit Ethernet, which is a standard LAN technology. The PCs run Linux as an operating system. Using a supercomputer such as IBM SP2 or Intel iPSC/860 in order to achieve the parallelism is more expensive and not necessarily faster.
With respect to domain decomposition, Fig. ![]() shows a result of using the METIS default routine
called kmetis. Experimenting with other METIS options did not
lead to any improvement. An important reason for this is that the
default options of METIS-4.0, which reduce the number of neighboring
processors one needs to communicate with, are exactly what we need for
our Beowulf cluster architecture.
shows a result of using the METIS default routine
called kmetis. Experimenting with other METIS options did not
lead to any improvement. An important reason for this is that the
default options of METIS-4.0, which reduce the number of neighboring
processors one needs to communicate with, are exactly what we need for
our Beowulf cluster architecture.
|
A so-called Gotthard scenario is a test for our simulations. In this scenario, we have a set of 50000 trips going to the same destination. Having all trips going to the same destination allows us to check the traffic jams on all used routes to the destination.
More specifically, the 50'000 trips have random starting points all over Switzerland, a random starting time between 6am and 7am, and they all go to Lugano. In order for the vehicles to get there, many of them should go through the Gotthard Tunnel. Thus, there are traffic jams at the beginning of Gotthard Tunnel, specifically on the highways coming from Schwyz and Luzern. This scenario has some similarity with vacation traffic in Switzerland.
Some snapshots can be viewed in Figure 4. The links with higher densities are indicated by darker pixels. Thus, the darker colored links are where the traffic jams are. The top left picture shows the case at 6:30am. As can be seen, the traffic is all over Switzerland. Therefore, there are not many congested links. In the top right figure, we see traffic at 7:30am where the vehicles are moving towards the highways. Since the vehicles coming from different towns are moving into the same highways, congestion is unavoidable and it is shown as the darker pixels.
The figure on the bottom left is the snapshot at 9:45am where most of the vehicles are on the main highways. In the bottom right snapshot, the simulation is near the end. The vehicles, that have passed through the Gotthard Tunnel, continue to Lugano and exit the simulation there. The Gotthard Tunnel and its immediate upstream links are indicated by darker pixels almost all the time except at the very beginning of the simulation.
Table 1 shows computing speeds for different numbers of CPUs for the queue simulation. This table shows the performance of the queue micro-simulation on a Beowulf Pentium cluster. The second column gives the number of seconds taken to run the first 3 hours of the Gotthard scenario. The third column gives the real time ratio (RTR), which is how much faster than reality the simulation is. A RTR of 100 means that one simulates 100 seconds of the traffic scenario in one second of wall clock time.
|
One could run larger scenarios at the same computational speed when using more CPUs. As the next step, we will be running our simulation on more realistic scenario which generates 10 million trips based on actual traffic patterns.
We would like to thank Andreas Völlmy for providing initial plan set data and Bryan Raney for the feedback he has given on this paper.
Here is an algorithm which selects a link with a probability
proportional to its capacity. It is a general algorithm which
selects proportional to weight when faced with ![]() items with
non-normalized weights
items with
non-normalized weights ![]() .
.

~karypis/metis/.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.47)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 1 -dir html ParallelQueueModel.tex
The translation was initiated by Kai Nagel on 2002-04-02