


Next: Some validation of the
Up: More realistic CA traffic
Previous: Introduction
Contents
The stochastic traffic cellular automaton (STCA)
The CA introduced in Chap. 7 can be made more general by
allowing vehicles to travel more than one cell per time step. Also,
it makes the simulation more realistic and more robust against
artifacts if one introduces some randomness. Both are achieved with
the following update rules:
- Car-following rule:
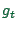 is the number of empty spaces to the car in front (``gap'');
is the number of empty spaces to the car in front (``gap'');
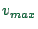 is the maximum velocity of the car under consideration.
is the maximum velocity of the car under consideration.
- Randomization:
- Moving:
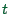 and
and 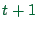 here refer to the actual time-steps of the simulation.
The first rule describes deterministic car-following: try to
accelerate by one velocity unit except when the gap is too small or
when the maximum velocity is reached.
here refer to the actual time-steps of the simulation.
The first rule describes deterministic car-following: try to
accelerate by one velocity unit except when the gap is too small or
when the maximum velocity is reached.
The second rule describes random noise: with probability 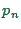 , a
vehicle ends up being slower than calculated deterministically. This
parameter simultaneously models three effects:
, a
vehicle ends up being slower than calculated deterministically. This
parameter simultaneously models three effects:
- Speed fluctuations during free driving: Assume a vehicle with no
other vehicles are nearby. It will eventually have speed
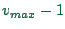 or
or 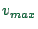 . In both cases,
. In both cases, 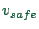 will be
will be 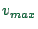 . After the
randomization, the speed will be at
. After the
randomization, the speed will be at 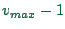 with probability
with probability
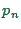 , and at
, and at 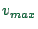 else. That is, the speed of a single
undisturbed vehicle fluctuates between
else. That is, the speed of a single
undisturbed vehicle fluctuates between 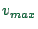 and
and 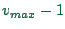 .
.
- Over-reactions at braking and car-following: Assume a vehicle
with
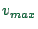 that approaches a slower vehicle from behind.
Eventually, it will reach a gap
that approaches a slower vehicle from behind.
Eventually, it will reach a gap
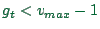 .
. 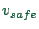 will
be equal to this
will
be equal to this 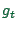 , and
, and 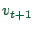 will either be equal to
will either be equal to 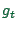 or
one smaller (without becoming negative). That is, with probability
or
one smaller (without becoming negative). That is, with probability
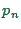 , the braking vehicle will not be at speed
, the braking vehicle will not be at speed 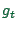 but slower.
but slower.
The argument for car following is similar: Assume a leading vehicle
with speed
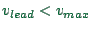 . The follower will attempt to follow
with
. The follower will attempt to follow
with
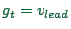 but in fact will fluctuate around that speed.
but in fact will fluctuate around that speed.
- Randomness during acceleration: Assume a single vehicle with
speed zero. Instead of acceleration
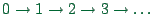 , the
acceleration will typically look like
, the
acceleration will typically look like
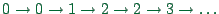 . Note that the rules are such that
the velocity never decreases during acceleration.
. Note that the rules are such that
the velocity never decreases during acceleration.
Obviously, these effects overlap to a certain extent; for example, if
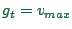 one cannot say if
one cannot say if 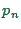 refers to car following or to
driving at free speed.
refers to car following or to
driving at free speed.
A translation into real-world units can be obtained as follows: The
length 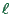 of a cell is given by the average space a car occupies
in a jam, since under jammed conditions each cell is filled by one
car. Thus,
of a cell is given by the average space a car occupies
in a jam, since under jammed conditions each cell is filled by one
car. Thus,
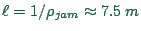 . A simulation time
step typically corresponds to one second in reality, and the order of
magnitude of this can be justified by reaction time arguments
(Sec. 27.4.1). One of the side-effects of this convention is
that space can be measured in ``cells'' and time in ``time steps'',
and usually these units are assumed implicitly and thus left out of
the equations. A speed of, say,
. A simulation time
step typically corresponds to one second in reality, and the order of
magnitude of this can be justified by reaction time arguments
(Sec. 27.4.1). One of the side-effects of this convention is
that space can be measured in ``cells'' and time in ``time steps'',
and usually these units are assumed implicitly and thus left out of
the equations. A speed of, say,  , means that the vehicle travels
five cells per time step, or 37.5 m/s, or 135 km/h, or approx.
85 mph.
, means that the vehicle travels
five cells per time step, or 37.5 m/s, or 135 km/h, or approx.
85 mph.
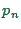 is often set to
is often set to 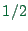 for theoretical work, while for realistic
traffic modelling
for theoretical work, while for realistic
traffic modelling 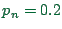 is a better choice.
is a better choice.
[[would be possible to show this in validation (more fdiags, as
function of params)]]



Next: Some validation of the
Up: More realistic CA traffic
Previous: Introduction
Contents
2004-02-02
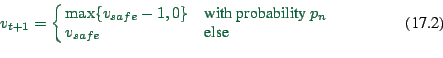

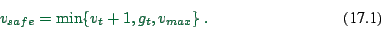
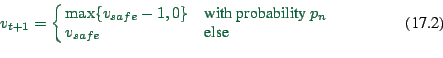

![]() , a
vehicle ends up being slower than calculated deterministically. This
parameter simultaneously models three effects:
, a
vehicle ends up being slower than calculated deterministically. This
parameter simultaneously models three effects:
![]() . The follower will attempt to follow
with
. The follower will attempt to follow
with
![]() but in fact will fluctuate around that speed.
but in fact will fluctuate around that speed.
![]() of a cell is given by the average space a car occupies
in a jam, since under jammed conditions each cell is filled by one
car. Thus,
of a cell is given by the average space a car occupies
in a jam, since under jammed conditions each cell is filled by one
car. Thus,
![]() . A simulation time
step typically corresponds to one second in reality, and the order of
magnitude of this can be justified by reaction time arguments
(Sec. 27.4.1). One of the side-effects of this convention is
that space can be measured in ``cells'' and time in ``time steps'',
and usually these units are assumed implicitly and thus left out of
the equations. A speed of, say,
. A simulation time
step typically corresponds to one second in reality, and the order of
magnitude of this can be justified by reaction time arguments
(Sec. 27.4.1). One of the side-effects of this convention is
that space can be measured in ``cells'' and time in ``time steps'',
and usually these units are assumed implicitly and thus left out of
the equations. A speed of, say, ![]() , means that the vehicle travels
five cells per time step, or 37.5 m/s, or 135 km/h, or approx.
85 mph.
, means that the vehicle travels
five cells per time step, or 37.5 m/s, or 135 km/h, or approx.
85 mph.
![]() is often set to
is often set to ![]() for theoretical work, while for realistic
traffic modelling
for theoretical work, while for realistic
traffic modelling ![]() is a better choice.
is a better choice.