Car following

Reaction time argument for car following

Any more realistic car micro-simulation first needs to have a method for simple car following. Such methods can be developed on single-lane loops, similar to a single-lane race track. A good way to start is the rule of thumb of ``two seconds time headway'', that many of us learn at driving school. We are supposed to have two seconds between the time when the car ahead passes a certain location, and the time when we pass it. The reason for this is related to our reaction time. If the car ahead starts braking really hard right when its back bumper is at that location, and if, after a reaction time, we start braking when our front bumper is at that same position, we will barely avoid a crash (see Fig. 27.3). Thus, time headway needs to be larger than reaction time, which translates into a space headway proportional to speed. As a consequence, most car following models have as their most important term one that makes the velocity a roughly linear function of the space headway or gap, although usually a reaction delay of one instead of two seconds is used.^27.3 All car following models based on this principle have a similar dynamical behavior. For example, the transition from laminar to start-stop traffic is similar for all these models (67). Car following models which are used in micro-simulations are usually designed to be free of accidents.

Figure 27.3: Reaction time argument. The left figure shows the trajectories of the front bumpers of two vehicles. At $t_1$, the leader starts breaking; at $t_2$, she has come to a standstill. The follower starts breaking at $t1 + t_{rct}$; and since his breaking follows exactly the same characteristics, he comes to a standstill at $t_2 + t_{rct}$. The right figure shows the same, with vehicle outlines superimposed. If at $t_1 + t_{rct}$, the follower's front bumper is beyond where the back bumper of the leader was when she started breaking, and accident cannot be avoided (but happens slightly later).

Discrete space and discrete time: Cellular automata rules

Incarnations of car following can use continuous or discrete time, and continuous or discrete space. While continuous space and continuous time is more realistic, discrete space and time are more natural for a digital computer. And recent research has shown that, in the spirit of Statistical Physics, extremely simple and even unrealistic rules on the microscopic level can still lead to reasonable behavior on the macroscopic level (78,79,90,19,66). In consequence, cellular automata (CA) techniques, which are discrete in space and time, plus have a parallel local update, can actually simulate traffic quite well. They also have a didactic advantage, since coding many aspects of traffic flow such as car following, lane changing, or gap acceptance, is straightforward with a CA approach.

Deterministic traffic CA

As already discussed in Secs. 7 and 17, typical CA for traffic represent the single-lane road as an array of cells of length $\ell$, each cell either empty or occupied by a single vehicle. Vehicles have integer velocities between zero and $v_{max}$. A possible update rule is (81)

(1)

$v_{t+1} = \min[ g , v_t + 1, v_{max} ]$

(2)

$x_{t+1} = x_{t} + v_{t+1}$

$g$ is the number of empty cells between the vehicle under consideration and the vehicle ahead, and $v$ is measured in ``cells per time step''.

As will be discussed below, this model has some important features of traffic, such as start-stop waves, but it is unrealistically ``stiff'' in its dynamics.

As also already discussed in Sec. 17, $\ell$ is the length a vehicle occupies in a jam, it is often taken as $\ell = 7.5~m$. In order to get realistic results, a time step of one second is a good choice (remember the reaction time), and then $v_{max}=5$ corresponding to 135 km/h is a good choice. In applications, $v_{max}$ can be set according to a speed limit on the link. Note that in the traffic CA community distances and speeds are often given without units, which means that they refer to ``cells'' or ``cells per time step'', respectively.

This rule is similar to the CA rule 184 according to the so-called Wolfram classification (128); indeed, for $v_{max}=1$ it is identical.

It turns out that, after transients have died out, there are two regimes (Figs. 27.4 and 27.5):

• Laminar traffic. All vehicles have gaps of $v_{max}$ or larger, and speed $v_{max}$. Flow in consequence is $q = \rho \, v_{max}$.

• Congested traffic. All vehicles have gaps of $v_{max}$ or smaller. It turns out that they allways have a speed equivalent to their gap. This means that $\sum v_i = \sum g_i = N_{veh} \times \left\langle g\right\rangle$. Since density $\rho = 1/(\left\langle g\right\rangle +1)$, this leads to
  

  $$q = \rho \, v = 1 - \rho \ .$$ (27.8)

  
  

The two regimes meet where $\rho \, v_{max} = 1 - \rho$, i.e. at

$$\rho_* = \frac{1}{v_{max}+1} \ .$$ (27.9)

This is also the point of maximum flow, with

$$q_{max} = \frac{v_{max}}{v_{max}+1} \ .$$ (27.10)

Figure 27.4: Space-time plot of deterministic CA. Each line a configuration of the simulated road; traffic goes from left to right; time is going downward. Numbers denote the velocity for the next movement (in cells per time step). TOP: Laminar traffic. BOTTOM: Congested traffic. Some trajectories are added to guide the eye. Note that the structures move backwards while the vehicles themselves move forwards. These structures are what the deterministic CA model generates in terms of traffic jams.

Figure 27.5: Fundamental diagram for the deterministic CA.

Stochastic traffic CA (STCA)

One can add noise to the CA model by adding a randomization term:

(1b)

With probability $p_{noise}$ do: $v_{t+1} = \max[ v_{t+1} - 1 , 0 ]$ ; the ``max'' is needed to prevent negative speeds.

This makes the dynamics of the model significantly more realistic (Fig. 27.6). $p_{noise}=0.5$ is a standard choice for theoretical work; as already discussed in Sec. 17.3, $p_{noise} = 0.2$ is more realistic with respect to the resulting value for maximum flow (capacity). The stylized fundamental diagram for the STCA looks the same way as the fundamental diagram for the deterministic CA, i.e. as Fig. 27.4. Despite the same shape, the value of maximum flow will however be much lower than with the deterministic CA: about $2000~veh/hr$ for the STCA with $v_{max}=5$ and $p_{noise} = 0.2$ (Fig. 17.1) in contrast to $5~veh/6~sec = 3000~veh/hr$ (Eq. 27.10) for the deterministic CA with $v_{max}=5$.

Slow-to-start rules for STCA

Real traffic may have a strong hysteresis effect near maximum flow; there is however no agreement among researchers if or under which circumstances this effect truly exists. If it exists, it looks as follows: When coming from low densities, traffic stays laminar and at free speed up to a certain density $\rho_2$ (see Fig. 27.7). Above that, traffic ``breaks down'' into start-stop traffic. When lowering the density again, however, it does not become laminar again until $\rho < \rho_1$, which is significantly smaller than $\rho_2$, up to 30% (63,64). This effect can be included into the above rules by making acceleration out of stopped traffic weaker than acceleration at all other speeds, for example by:

• if $\Big( v_t=0$ and $g_t \le 1 \Big)$ then $v_{t+1} = 0$

• else $v_{t+1} = \min[ g_t , v_t + 1, v_{max} ]$.

This means that the vehicle needs a larger $g$ than before to start moving. Such rules are called ``slow-to-start'' rules in the physics community (31,7).

Figure 27.6: Space-time plot of stochastic CA. Each line is a configuration of the simulated road; traffic goes from left to right; time is going downward. TOP: Laminar traffic. BOTTOM: Jam out of nowhere leading to congested traffic.

Figure 27.7: Stylized fundamental diagram for slow-to-start STCA.

Time-oriented CA (TOCA)

A modification to make the STCA more realistic is the so-called time-oriented CA (TOCA) (19). The motivation is to introduce a higher amount of elasticity in the car following, that is, vehicles should accelerate and decelerate at larger distances to the vehicle ahead than in the STCA, and resort to emergency braking only if they get too close. For the TOCA velocity update, the following operations need to be done in sequence for each car:

1. if ( $g > v \cdot \tau_H$ ) then, with probability $p_{ac}$,
   

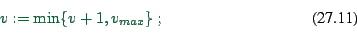   $$v := \min\{ v+1, v_{max} \} \ ;$$ (27.11)

   
   

2. $v := \min\{ v, g \}$

3. if ( $g < v \cdot \tau_H$ ) then, with probability $p_{dc}$,
   

   $$v := \max\{ v-1, 0 \} \ .$$ (27.12)

   
   

Typical values for the free parameters are $(p_{ac},p_{dc},\tau_H) = (0.9,0.9,1.1)$. The TOCA generates more realistic fundamental diagrams than the original STCA, in particular when used in conjunction with lane-changing rules on multi-lane streets.

Dependence on the velocity of the car ahead

It makes sense to assume that velocity difference between vehicles should be included. The idea is that if the car ahead is faster, then this adds to one's effective gap and one may drive faster than without this. In the CA context, the challenge is to retain a collision-free parallel update. Wolf (127) achieves this by going through the velocity update twice, where in the second round any major velocity changes of the vehicle ahead are included. Barrett et al. (11) instead additionally look at the gap of the vehicle ahead. The idea here is that, if we know the gap of the vehicle ahead, and we make assumptions about the driver behavior of the vehicle ahead, then we can compute bounds on the behavior of the vehicle ahead in the next time step.

Theory

CA rules can also be analyzed analytically, by means of statistical techniques which look at sequences of configurations of the dynamical evolution of the system (e.g. 106,30,105). Note that this is possible because the cellular approach makes the dynamical states countable: There is only a finite number of possible states for a given number of cells.

Continuous space and continuous time

Making both space and time continuous results in coupled differential equations. Such models for car following were established quite some time ago (e.g. 48, and references therein). Most of them also use in one way or other the reaction time argument of Sec. 27.4.1 (as they should). For example, one could use

$$v(t+\tau) = \alpha \, \Delta x(t) \ ,$$ (27.13)

where $\Delta x$ is the distance to the car ahead.^27.4 This just means that, after some time delay, our velocity is proportional to $\Delta x$, as it should be according to the reaction time argument.

One can expand $v(t+\tau) = v(t) + \tau \, \dot v(t) + ...$, drop second order terms, and rearrange, resulting in

$$\dot v(t) = {1 \over \tau} \, \Big( \alpha \, \Delta x(t) - v(t) \Big)$$ (27.14)

That is, we adjust our velocity change so that we are adjusting towards the ``correct'' velocity $v = \alpha \Delta x$. Eqs. (27.13) and (27.14) do not in general generate the same dynamics, in spite of having the same dynamic origin.

A generalization of Eq. (27.14) is to replace $\alpha \, \Delta x_t$ with a function $V(\Delta x(t))$:

$$\dot v(t) = {1 \over \tau} \, \Big( V(\Delta x(t)) - v(t) \Big)$$ (27.15)

We will need this again later.

[[bando ref]]

The ``classic'' car-following model family (48) comes from taking a time-derivative of the reaction-time relation Eq. (27.13), leading to

$$\dot v(t+\tau) = \alpha \Delta v(t) \ .$$ (27.16)

After adding some more or less plausible prefactors, this leads to

$$\dot{v}(t+\tau) = \alpha \, \frac{[v(t+\tau)]^l}{ [\Delta x(t)]^m } \, \Delta v(t) \ .$$ (27.17)

These models are however unstable (e.g. 89). The reason behind that is that they allow vehicles to follow each other at extremely close distances with very high speeds as long as there is no velocity difference between them: From $\Delta v=0$ follows $\dot v = 0$. Once a small velocity difference shows up, they react with violent fluctuations. Note that neither Eq. (27.13) nor (27.14) allow such a solution.

For computer implementations, models with continuous time are inconvenient, since time needs to be discretized in one way or other. Because of the reaction delay, many of these car-following equations are delay equations, where considerable effort needs to be spent for faithful numerical results. Given this observation, it seems to be simpler to build models that use discretized time to their advantage (see next section). This is not to say that continuous car-following models are useless; indeed, they continue to contribute to our understanding of the matter (e.g. 6,5). We would expect, however (see below), that any faithful discretization of these equations will run a lot more slowly on a computer than the model presented in the next section, which explicitly uses discrete time.

Another possible implementation of continuous space and time would be event-driven. This works best when particles move with constant velocity for periods of time, interrupted by events where they change it. Molecular dynamics with hard core interactions is an example. Since human driving behavior can probably indeed be characterized like that (125), this should be a promising approach. However, parallel implementations of event-driven simulations are hard and therefore large scale simulations currently not done with this method.

Discrete time and continuous space car following

A disadvantage of the CA approach to traffic is that the coarse-gained description makes fine tuning of many properties difficult. For example, it is difficult to represent fine-grained differences in speed limits, or different acceleration profiles.

On the other hand, the use of coupled ordinary differential equations turns out to be inconvenient for traffic simulations, in particular because of the explizit handling of the reaction time, which means that for numerical integration one needs to maintain the entire dynamical history between $t$ and $t - \tau$ in increments of the time discretization $\Delta t$. There are however also models that are continuous in space but coarse-grained discrete in time which work extremely well for traffic (49,104,131,68,66). The reason for this is that drivers have a reaction delay of about one second, and it is advantageous to use this reaction delay as the time step for the micro-simulation. From a practical point of view, traffic models which use discrete time but continuous space are numerically as efficient as the CA models but are much easier to calibrate. Obviously, a multitude of models is possible here - as is with CAs. We want to concentrate on a single model, a model described by Krauß (68,66). This model is particularly well understood.

The approach starts again from the reaction time argument (Sec. 27.4.1), this time taking into account the possibility that the two cars can have different velocities. This results in the condition that one's braking distance plus the distance that one drives until one reacts should be smaller than the braking distance of the car ahead plus the space in between the two vehicles. Formally, this yields

$$d(v) + v \, \tau \leq d(\tilde v) + g \ ,$$ (27.18)

where $d(v)$ is the braking distance of a car moving with speed $v$, $\tau$ is the reaction time, $g$ is the distance to the car ahead, and $\tilde v$ is the speed of the car ahead (``leader'').^27.5

This can be used to derive (see Fig. 27.8) a simple update scheme for the dynamical state of a car:

$$v_{\rm safe} = \tilde v_t + \frac{g_t - \tilde v_t\tau}{\overline{v}/b + \tau}$$ (27.19)

$$v_{\rm des} = \min \{ v_t + a \, h, v_{\rm safe} , v_{\rm max} \}$$ (27.20)

$$v_{t+h} = \max \{ 0 , v_{\rm des} - \epsilon \, a \, \eta \}$$ (27.21)

$$x_{t+h} = x_t + h \, v_{t+h}\ .$$ (27.22)

$\overline v = (v + \tilde v)/2$ is the average velocity of the two cars involved, $a$ is the maximum acceleration of the vehicles, $b$ their maximum deceleration, $\epsilon$ is the noise amplitude, and $\eta$ is a random number following a flat distribution in $[0,1]$.

Figure 27.8: Derivation of the model by Krauss.

The terms can be interpreted as follows:

• The first rule (i.e. Eq. 27.19) can be rewritten as
  

  $$v_{safe} = \alpha \, \frac{g_t}{\tau} + (1-\alpha) \, \tilde v_t$$ (27.23)

  
  
  with
  

  $$\alpha = \frac{1}{\overline{v}/(b \, \tau) + 1} \ .$$ (27.24)

  
  
  [[check on paper]] That is, $v_{safe}$ is a weighted average of $g/\tau$ and $\tilde v$. For $\alpha < 1$, the velocity of the car ahead is added to the calculation in the following way: If the car ahead is faster, then one can be a little faster than allowed by the gap alone; if the car ahead is slower, then one needs to be slower than allowed by the gap alone.

  Note that for $\alpha = 1$ and $\tau = 1$ we recover the STCA rule.

• The second rule (i.e. Eq. (27.20)) just states that the velocity is limited by the desired acceleration $a$, by the safe velocity $v_{\it safe}$ as calculated above, and by the maximum velocity $v_{\it max}$.

  Note that this is the same as the CA rule.

• In the third term, noise $\eta$ is added by randomly making the vehicle slower than so far calculated. $\eta$ denotes a random variable between zero and one, $\epsilon$ is a noise scaling factor.

  Again, this is the same as the CA rule.

• The fourth term denotes the forward movement.

For $h \le \tau$ one can show that this model is free of collisions (Fig. 27.8); normally, one uses $h = \tau$. Typical values for $(a,b,\epsilon)$ are $(0.2,0.6,1)$.