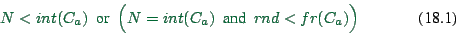


Next: Fair intersections
Up: The queue model for
Previous: Introduction
Contents
From our general framework, we have the following requirements to a
traffic simulation:
- Vehicles need to be able to follow plans. This implies that the
simulation needs to be dynamic (i.e. time-dependent), and that some
notion of individual vehicles needs to be present in the simulation.
- The simulation needs to be reasonably fast. A computational
speed of at least 100 times faster than real time (i.e. simulating
24 hours of traffic in 0.24 hours of computing time) is desirable in
order to obtain bearable waiting times for the feedback/learning.
This computing speed can be achieved by selecting small scenarios, by
using simple models, or by parallel computing. This text concentrates
on the last two aspects.
The important numbers characterizing a road from the perspective of
transportation planning are:
- Free speed. This is the speed that vehicles drive on a
link when no other constraints are present.
- Flow capacity. This is the maximum number of vehicles per
time unit that can move over a link when no other constraints are
present. In city traffic, the flow capacity is often determined by a
traffic light at the end.
- Storage constraint. This is the maximum number of
vehicles that can be on a link under jammed conditions.
The first two numbers are also used in all traditional transportation
planning software (based on static assignment, see
Chap. 28) and are therefore typically available with
standard data files for transportation planning. The third number is
necessary when a link is full and no more vehicles can enter, causing
spillback. Without the storage constraint, flow demand above the flow
capacity would allow an unlimited number of vehicles on the link,
which is clearly not realistic.
The queue model bases its dynamics on free speed, flow capacity, and
storage constraint only.
Typical input data are, for each link 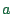 , the attributes free flow
velocity
, the attributes free flow
velocity 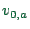 , length
, length 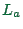 , capacity
, capacity 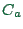 and number of lanes
and number of lanes
 .
Free flow travel time is calculated by
.
Free flow travel time is calculated by
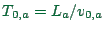 .
The storage constraint of a link is calculated as
.
The storage constraint of a link is calculated as
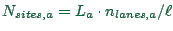 , where
, where 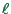 is the space a single vehicle
in the average occupies in a jam, which is the inverse of the jam
density. One can use
is the space a single vehicle
in the average occupies in a jam, which is the inverse of the jam
density. One can use
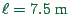 , as for the CA technique.
, as for the CA technique.
The arguably simplest intersection logic (47) is that
all links are processed in arbitrary but fixed sequence, and a vehicle
is moved to the next link if (1) it has arrived at the end of the
link, (2) it can be moved according to capacity, and (3) there is
space on the destination link (see Algorithm A in Fig. 18.1).
More formally, the following happens:



Next: Fair intersections
Up: The queue model for
Previous: Introduction
Contents
2004-02-02
![]() , the attributes free flow
velocity
, the attributes free flow
velocity ![]() , length
, length ![]() , capacity
, capacity ![]() and number of lanes
and number of lanes
![]() .
Free flow travel time is calculated by
.
Free flow travel time is calculated by
![]() .
The storage constraint of a link is calculated as
.
The storage constraint of a link is calculated as
![]() , where
, where ![]() is the space a single vehicle
in the average occupies in a jam, which is the inverse of the jam
density. One can use
is the space a single vehicle
in the average occupies in a jam, which is the inverse of the jam
density. One can use
![]() , as for the CA technique.
, as for the CA technique.