Limitations of the queue model

In the introduction to this chapter, it was pointed out that the queue simulation is eventually limited in terms of its realism. In this section, these limitations will be discussed.

A first limitation concerns the dynamics of traffic jams. In the queue model, when a vehicle leaves a link, that free spot becomes available for entering vehicles very quickly: In Algorithm A, it becomes available immediately; in Algorithm B, it is somewhat delayed by the buffer dynamics and the parallel update. In both cases, however, the time that it takes until it becomes available for entering vehicles does not depend on the link length. This is in stark contrast to reality, where such ``holes'' travel with a finite speed of approximately 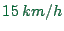$15~km/h$. The reason for the real-world behavior becomes immediately obvious if one looks at the corresponding dynamics in the CA, where a hole in a completely dense jam is slowly passed on against the traffic direction by at most one vehicle movement in each time step; this is discussed in more detail in Chap. 27.

This limited realism in terms of traffic jam dynamics shows up when solid jams in the queue model, for example caused by an accident, are dissolved: Instead of being dissolved at the downstream end only, such jams in the queue model are dissolved quasi-simultaneously along the whole length. [[fig portland]] It seems however that this problem can be resolved via additional rules, such as a limitation on the ``speed of holes'' ().

Other limitations are concerned with the limited vehicular and spatial resolution:

• Interaction between slow and fast vehicles. On multi-lane roads, fast cars can pass slow cars as long as traffic is light. Only when traffic becomes denser, then fast cars are caught between slow cars. In the queue simulation, all cars are assumed to drive with the same speed.

• Interaction between different vehicle types. Examples for this are interactions between pedestrians and cars, bicycles and cars, or between buses/light rail and cars.

• Signal phases. Diligent signal phasing can make an enormous difference to an intersection capacity. This cannot be captured by simple intersection capacities, since it depends on how traffic streams and signal phases work together.

• Complicated street layouts. Merging, turning, and weaving lanes make a substantial difference to traffic flow. Most importantly, turning lanes, i.e. the separation of vehicle streams by turning direction, prevents situations such as in Fig. 18.4, where a left turning vehicle blocks all the traffic behind it. This becomes particular important in conjunction with signal phases, since optimally the turning lanes are emptied out during each green phase. That is, turning lanes of the correct length ensure that the green phases of an intersection are used optimally.

• Weaving, in particular if large numbers of vehicles enter a street on the right lane(s) but want to exit it on the left lane(s).

For such effects, the simple queue simulation is no longer sufficient. Sometimes, parameterizations of certain effects are available, but in general it will be necessary to resort to a more realistic type of micro-simulation. In such a more realistic micro-simulation, one will not only have individual cars with different individual characteristics, but also realistic street layouts, signals, bicycles, pedestrians, light rail and buses, etc.

Figure 18.4: Problem of FIFO-based models