

Next: Constrained optimization
Up: Static assignment
Previous: Equilibrium principle
Contents
Define a function
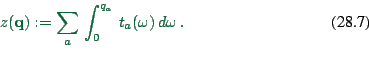 |
(28.7) |
The sum is over all links 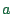 ; for each link, we integrate over the
travel time as flow increases, up to the flow
; for each link, we integrate over the
travel time as flow increases, up to the flow 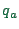 actually used on
that link.
actually used on
that link.
This is a function which maps high-dimensional space into a scalar
number. The number of dimensions is the number of links in the network.
I am not aware of an intuitive motivation for this function. It just
turns out that it works: Minimization of this function subject to
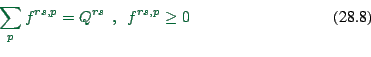 |
(28.8) |
and together with the definitions from above gives the desired
equilibrium solution. This is actually not too hard to show.
However, the derivation does not give any intuitive insight why
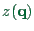 is the correct function.
is the correct function.
With this transformation, the equilibrium problem is transformed into
a constrained optimization problem. Optimization problems are in
general much better understood than equilibrium problems.



Next: Constrained optimization
Up: Static assignment
Previous: Equilibrium principle
Contents
2004-02-02