 |
(28.1) |
 |
(28.2) |
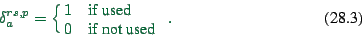 |
(28.3) |
 |
(28.4) |
 |
(28.5) |
The steady state assignment of electric or water currents to a network follows an equilibrium principle: Along any path through the network, the sum of the voltages is the same. This means that the amount of energy (cost) necessary to go from one point in the network to another one does not depend on the path.
For traffic, the situation is similar, except that our particles have destinations. We thus characterize particles/streams by their (origin,destination) (OD). Only particles which have the same origin and the same destination are treated as interchangeable.
The equilibrium principle is stated as
Under equilibrium conditions traffic arranges itself in such a way that no individual trip maker can reduce his/her path costs by switching routes.This is Wardrop's (first) principle.
If all trip makers perceive the same cost functions, then one can move the point of view from individual travelers to OD flows:
Under equilibrium conditions traffic arranges itself such that all used routes between an OD pair have equal costs while all unused routes have a cost equal to that or greater.
The idea behind this is: If, for a given OD pair, there is a faster path, then people will start using it, thus making it slower. This process will stop once the new path is as slow as the other paths which are used for this OD pair.
For a mathematical formulation, one needs notation:
 |
(28.1) |
 |
(28.2) |
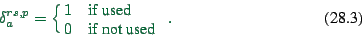 |
(28.3) |
 |
(28.4) |
 |
(28.5) |
The translation of Wardrop's equilibrium principle into our new
notation means that we we are searching for an assignment of the OD
streams to the network so that we have
 |
(28.6) |