Maximum likelihood estimation

Situation:

Have survey of $n=1..N$ persons, and options $A$, $B$.

Also have attributes $x_{n,A,1}$, $x_{n,A,2}$, ... $= \vec x_{n,A}$ as well as $x_{n,B,1}$, $x_{n,B,2}$, ... $= \vec x_{n,B}$.

[This means for example that we know the ``time by bus'' even if the person never tried that option.]

Note that we now have a person index $n$ everywhere.

Also have model specification

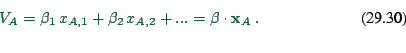$$V_A = \beta_1 \, x_{A,1} + \beta_2 \, x_{A,2} + ... = \vec \beta \cdot \vec x_A \ .$$ (29.28)

How to find $\beta_1,...,\beta_k$?

... for binary choice in general

Assume set of persons $n=1..N$ that were asked.

$y_{n,A} = 1$ means person $n$ chose option $A$. (Implies that $y_{n,B} = 0$.)

Assuming that we have our model, what is the proba that persons $(1,2,3,4,...)$ make choices $(A,B,A,A,...)$? It is (as usual, assuming that the choices are indep)

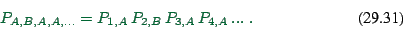$$P_{A,B,A,A,...} = P_{1,A} \, P_{2,B} \, P_{3,A} \, P_{4,A} \, ... \ .$$ (29.29)

Using the $y_{n,B}$:

$$P_{survey} = \prod_n P_{n,A}^{y_{n,A}} \, P_{n,B}^{y_{n,B}} \ .$$ (29.30)

We want, via varying the $(\beta_1,...,\beta_k)$, to maximize this function.

In words, again: Want high probability that survey answers would come out of our model.

Maximizing in 1d means: Set first derivative to zero, and check that second derivative negative.

Maximizing in multi-d means: Set all first partial derivaties to zero; check that matrix of mixed second derivaties is negative semi-definite.

Instead of maximizing the above function, we can maximize its log (monotonous transformation). Usual trick with probas since it converts products to sums.

$$L = \log P_{survey} = \sum_n [ y_{n,A} \, \log P_{n,A} + y_{n,B} \, \log P_{n,B} ] \ .$$ (29.31)

So far this is general; next it will be applied to Logit.

... for binary logit model

(Remember: ``Logit'' means ``Gumbel distributed randomness''.)

Strategy: Replace $P_{n,X}$ in Eq. (29.39) or in Eq. (29.40) by specific from of logit model, i.e.

$$P_{n,X} = \frac{e^{\vec \beta \cdot \vec x_X}}%% {e^{\vec \beta \cdot \vec x_A} + e^{\vec \beta \cdot \vec x_B}}$$ (29.32)

and then find values $\beta_i$ such that $P_{survey}$ or $L$ are maximized.

Computer science solution

From a computer science perspective, the maybe easiest way to understand this is to just define a multidimensional function in the variables $\beta_0, \beta_1, ...$ and then to use a search algorithm to optimize it.

This function would essentially look like

{}
double psurvey ( Array beta ) {
    double prod = 1. ;
    for ( all surveyed persons n ) {

        // calculate utl of option A:
        double utlA = 0. ;
        for ( all betas i ) {
            // utl contrib of attribute i:
            utlA += beta[i] * xA[n,i] ; 
        }
        double expUtlA = exp( utlA ) ;

        // calculate utl of option B:
        double utlB = 0. ;
        for ( all betas i ) {
            // utl contrib of attribute i:
            utlB += beta[i] * xB[n,i] ; 
        }
        double expUtlB = exp( utlB ) ;

        // contribution to prod:
        if ( person n had selected A ) {
            prod *= expUtlA/(expUtlA+expUtlB) ;
        } else {
            prod *= expUtlB/(expUtlA+expUtlB) ;
        }

    }
    return prod ;
}

Search algorithms could for example come from evolutionary computing.

The ``computer science'' way is almost certainly more computer intensive and less robust than the conventional strategy, lined out next. It does however have the advantage of being applicable also to cases where the conventional strategy fails.

Conventional strategy

The conventional strategy, mathematically more sound but also conceptually somewhat more difficult, is to first invest everything that one knows analytically and only then use computers.

The analytical knowledge mostly involves that one can search for maxima in high-dimensional differentiable functions by first taking the first derivative and then setting it to zero. This is lined out in the following.

Preparations

Define In consequence and (Left version is sometimes useful.)

First derivative of $\log P_{n,A}$:

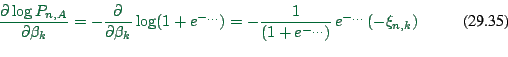$$\frac{\partial \log P_{n,A}}{\partial \beta_k} = - \frac{\pa... ....} ) = - \frac{1}{(1 + e^{-...})} \, e^{-...} \, (- \xi_{n,k})$$ (29.33)

or Similarly

We will also need

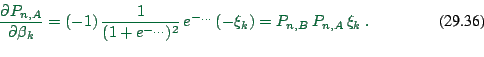$$\frac{\partial P_{n,A}}{\partial \beta_k} = (-1) \, \frac{1}... ...^2} \, e^{-...} \, (-\xi_k) = P_{n,B} \, P_{n,A} \, \xi_k \ .$$ (29.34)

Core calculation

Now we can do

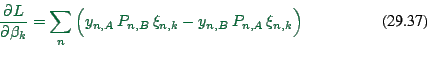$$\frac{\partial L}{\partial \beta_k} = \sum_n \Big( y_{n,A} \, P_{n,B} \, \xi_{n,k} - y_{n,B} \, P_{n,A} \, \xi_{n,k} \Big)$$ (29.35)

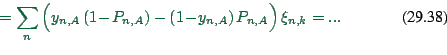$$= \sum_n \Big( y_{n,A} \, (1\!-\!P_{n,A}) - (1\!-\!y_{n,A}) \, P_{n,A}\Big) \, \xi_{n,k} = ...$$ (29.36)

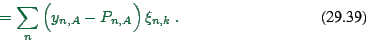$$= \sum_n \Big( y_{n,A} - P_{n,A} \Big) \, \xi_{n,k} \ .$$ (29.37)

When replacing $P_{n,A}$: Very good. Now remember that we need to set this, simultaneously for all $k$, equal to zero in order to obtain the values for $\vec\beta$ which maximize $L$.

(E.g. Newton in higher dimensions.)

Uniqueness (no contribution to understanding)

Need to check that this is a max (and not a min), and that it is the global max and not a local one.

Reminder: 1d function has max if 1st derivative is zero and 2nd deriv is negative. If 2nd deriv is globally negative, then this is the also the global max.

Translation to higher dimensions: Matrix of 2nd derivatives is globally negative semidefinite.

$M$ negativ semidefinite: $x^T C x > 0$ except for $x=0$.

Note: Assume $C = M^T \, M$. Then $x^T M^T M x = (M x)^T \, (M x) > 0$ except for $x=0$ as long as all entries of $M x$ are real (i.e. not complex).

Now

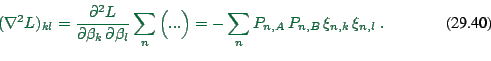$$(\nabla^2 L)_{kl} = \frac{\partial^2 L}{\partial \beta_k \, ... ...g) = - \sum_n P_{n,A} \, P_{n,B} \, \xi_{n,k} \, \xi_{n,l} \ .$$ (29.38)

Def

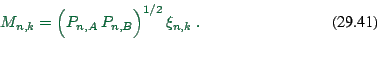$$M_{n,k} = \Big( P_{n,A} \, P_{n,B} \Big)^{1/2} \, \xi_{n,k} \ .$$ (29.39)

Then

$$\nabla^2 L = - M^T \, M \ .$$ (29.40)

Since all entries of $M$ are real, $M^T \, M$ is positive definite, and therefore $- M^T \, M$ negativ definite.