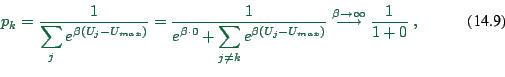Departure time selection

In general, one would assume that travelers select the departure time with the largest utility. Let us however assume that the above utility calculation is somewhat fuzzy, for example because travelers do not know the different contributions exactly. Then, we want that the probability to select a certain departure time grows with the respective utility.

A typical mathematical form to achieve this if one has to select between several different options $i$ is

$$p_i \propto e^{ \beta U_i } \ .$$

Since $p_i$ is a probability, this needs to be normalized, i.e. one wants $\sum_i p_i = 1$, where the sum goes over all possible options. This results in

$$p_i = \frac{ e^{\beta U_i} }{ \sum_j e^{\beta U_j} } \ ,$$

where the sum in the denominator goes over all possible options including $i$.

Note that this mathematical form does exactly what we want: if $U_i$ is large, then option $i$ has a high probability of being selected. The parameter $\beta$ changes the randomness of this choice.

• If $\beta \to 0$, then the choice does not depend on the $U_j$; in consequence, it is totally random with equal weight on each option.

• If in contrast $\beta \to \infty$, then the option with the highest utility will be selected with probability one, and all others will never be selected.

  One way to see this is the following. Assume that $U_{max}$ is the largest utility, and let us assume that there is only one optimal choice (to simplify the argument). First let us look at a non-optimal choice $i$, i.e. $U_i < U_{max}$. Then
  

  $$p_i = \frac{e^{\beta U_i}}{e^{\beta U_{max}} \, \sum_j e^{ ... ..._j - U_{max}) }} < \frac{e^{\beta U_i}}{e^{\beta U_{max}}} \ ,$$
  
  
  since the sum is larger than one. (One of the contributions comes from $U_j = U_{max}$, and all other contributions are positive.) This can be rewritten as
  
  $$e^{\beta (U_i - U_{max})} \stackrel{\beta \to \infty}{\too} 0$$
  
  
  (because $U_i - U_{max} < 0$).

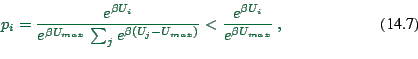
  Now let us look at the optimal choice $k$, i.e. $U_k = U_{max}$. Then
  

  $$p_k = \frac{1}{\displaystyle \sum_j e^{\beta (U_j - U_{max}... ...{max})}} \stackrel{\beta \to \infty}{\too} \frac{1}{1 + 0} \ ,$$
  
  
  because $U_j - U_{max} < 0$ for $j \ne k$.