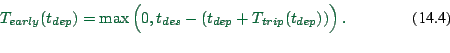


Next: Departure time selection
Up: Activities planner: Adjust trip
Previous: Introduction
Contents
Subsections
These trade-offs are operationalized via giving utitilies to the
different aspects of the situation. The utilities in this chapter
will be negative, which is why they are sometimes called disutilities.
Let us assume that we have the following utilities:
- The (dis)utility of the trip time,
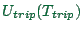 . It
depends on the trip time,
. It
depends on the trip time, 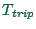 .
.
- The (dis)utility of being early,
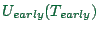 . It
depends on how early the traveler is. If the traveler is late, this
contribution is zero.
. It
depends on how early the traveler is. If the traveler is late, this
contribution is zero.
- The (dis)utility of being late,
 . It
depends on how late the traveler is. If the traveler is early, this
contribution is zero.
. It
depends on how late the traveler is. If the traveler is early, this
contribution is zero.
Let us further assume that these utilities are additive (see
Fig. 14.1):
An example is:
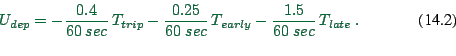 |
(14.1) |
The results of this come out in arbitrary utility units, sometimes
called ``utils''.
Fig. 14.1 gives the function of the different utilities
as a function of the arrival time. For the calculation that we
will do later, we need them as a function of departure time.
For example, if 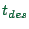 is the desired arrival time, then
is the desired arrival time, then
Here, 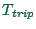 again depends on
again depends on 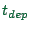 , and therefore
, and therefore
As we will see later, we will essentially need a table of the
values of 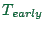 as a function of
as a function of 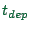 where
where 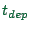 increases in 5-min time steps. Because of this simplification, the
problem can be solved as a sequence of look-ups, resulting in a table
similar to the following (where
increases in 5-min time steps. Because of this simplification, the
problem can be solved as a sequence of look-ups, resulting in a table
similar to the following (where
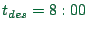 )
)
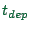 |
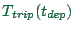 |
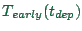 |
| 6:00 |
0:15 |
1:45 |
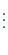 |
|
|
| 7:00 |
0:15 |
0:45 |
| 7:05 |
0:19 |
0:36 |
| 7:10 |
0:30 |
0:20 |
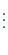 |
|
|
Figure 14.1:
Utility contributions
|
|



Next: Departure time selection
Up: Activities planner: Adjust trip
Previous: Introduction
Contents
2004-02-02

![]() is the desired arrival time, then
is the desired arrival time, then