Departure time choice

Now the departure time needs to be chosen for each individual traveler. For this, it is easiest to continue with the code written in Sec. 14.6 (Task 14.2). After retrieving the travel time information from the events file, the code will start reading the 10% activities file produced in Sec. 14.5. For each agent it will retreive a pair of activities. The desired arrival time $t_{des}$ comes from there as discussed above. For each activity pair in the activities file do:

Retrieve or calculate, for each departure time $t_{dep}$ between 5am and 10am in 5min steps, the following quantities:

the trip time $T_{trip}$;

the arrival time $t_{arr}$;

the early time $T_{early} = \max[ 0, t_{des}-t_{arr} ]$;

the late time $T_{late} = \max[ 0, t_{arr} - t_{des} ]$;

the resulting utility

$$U_{dep} = - \frac{0.4}{60~sec} \, T_{trip} - \frac{0.25}{60~sec} \, T_{early} - \frac{1.5}{60~sec} \, T_{late}$$

(this is the same as Eq. (14.2));

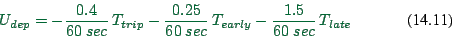
and the resulting non-normalized probability

$$\pi_i = e^{U_{dep}} \ .$$

Once you have done this for all time bins, sum up all the non-normalized probabilities:

$$\Pi := \sum_i \pi_i \ .$$

Divide all non-normalized probabilities by this value:

$$p_i := \pi_i / \Pi \ .$$

Make a random draw between these probabilities (see below) and note the resulting departure time.

Fuzzify the departure time by $\pm 150$sec (2.5min) by something like

{}
TDepInSec = TDepInSec - 150 + int( 300*MyRand() ) ;

Write out the corresponding trip.

All trips then need to be routed; this is done by applying the time-dependent router to the trips file as before.

We need to make a random draw according to the probability weights. This is for example done as follows. Assume that we have p[i], i=1..N given, with the sum of these $p[i]$ being one. Then do something like the following:

{}
double rnd = myRand() ;
double sum = 0. ;
int ii ;
for ( ii=1; ii<=N; ii++ ) {
    sum += p[ii] ;
    if ( sum > rnd ) break ;
}
// ii is the desired index.

Task 14.3   Take the events file from the 50th iteration of the corridor problem. Generate, for travelers 1-250 in

        http://www.matsim.org/files/studies/corridor/teach/0.acts ,

the departure times ($=$ new trips). Plot the resulting new departure time distribution (see below). Does this correspond to your expectations? Why (or why not)?

Note: Departure time distribution means that on the x-axis you have the departure time, and on the y-axis you have how many vehicles/travelers depart at that time. For this, you again need to introduce time bins, for example 5 minutes wide.