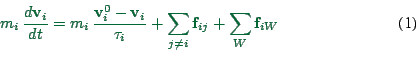 |
(1) |
As mentioned above, the mobility simulation takes care of the physical aspects of the system, such as interaction of the agents with the environment or with each other. Typical simulation techniques for such problems are:
For our simulations, we need to maintain individual particles, since they need to be able to make individual decisions, such as route choices, throughout the simulation. This immediately rules out field-based methods. We also need a realistic representation of inter-pedestrian interactions, which rules out both the queue models and the SPH models.
For microscopic simulations, there are essentially two techniques:
methods based on coupled differential equations, and cellular automata
(CA) models. In our situation, it is important that agents can move
in arbitrary directions without artifacts caused by the modeling
technique, which essentially rules out CA techniques.
A generic coupled differential equation model for pedestrian movement
is the social force model (Helbing et al., 2000)
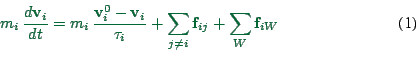 |
(1) |
The specific mathematical form of the interaction term does not seem
to be critical for our applications as long as it decays fast enough.
Fast decay is important in order to cut off the interaction at
relatively short distances. This is important for efficient
computing, but it is also plausible with respect to the real world:
Other pedestrians at, say, a distance of several hundred meters will
not affect a pedestrian, even if those other pedestrians are at a very
high density. We use an exponential force decay of
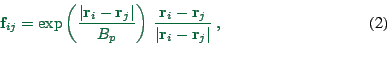 |
(2) |
The main problem with existing pedestrian models for our purposes is
that they do not work when confronted with such large areas as are
necessary to cover a complete hiking area: Covering an area of
![]() area (necessary to allow hikes of length
area (necessary to allow hikes of length ![]() in all
directions from a central starting point) with cells of
in all
directions from a central starting point) with cells of ![]() results in
results in ![]() cells, which needs at least
cells, which needs at least ![]() of memory.
This makes the straightforward application of a technique based on
cells impossible. Models based on continuous coordinates have the
similar problem that all objects need to be represented, and again a
straightforward implementation goes beyond available computer memory.
All models have the problem that long-distance path following has
never been looked at, at least not to our knowledge.
of memory.
This makes the straightforward application of a technique based on
cells impossible. Models based on continuous coordinates have the
similar problem that all objects need to be represented, and again a
straightforward implementation goes beyond available computer memory.
All models have the problem that long-distance path following has
never been looked at, at least not to our knowledge.
We introduced (Gloor and Nagel, 2002; Mauron, 2002) a model that uses only sparse information which fits into computer memory, runs efficiently on our scenarios, and has agents follow paths without major artifacts. This model will be described in the following.
For our simulation, we need to assume that the geometry is given by a graph (network) of hiking path plus some terrain features, and that the desired velocity of the hiker is consistent with this graph. The maybe first implementation that comes to mind is as follows:
However, this approach has the disadvantage that, close to a way-point, agents are artificially pulled towards that way-point even if that does not make sense (see Fig.4). This could be avoided by switching to the next way-point before actually reaching this way-point, but then without special measures pedestrians may not be able to execute a switchback, because the next way-point may pull them back on the current segment. Also, the approach quite in general does not work once curved segments are allowed between way-points.
We developped a more specialized approach (Gloor and Nagel, 2002; Mauron, 2002), in which this artefacts do not exist. Our model uses a path-oriented coordinate system (see Fig. 5) for the computation of the desired velocity. It also uses a so-called path-force, which pulls the agents back on the path when he moves away from its center (e.g. due to interaction with other agents or obstacles). Fig. 6 demonstrates that the new approach keeps the pedestrians on their side of the path even in the vicinity of way-points.
![\includegraphics[width=0.8\hsize]{model0.waypoints-gz.eps}](img27.png)
|
![\includegraphics[width=0.8\hsize,clip=true,viewport=0cm 0cm 12cm 5.5cm]{bfield-gz.eps}](img28.png)
|
![\includegraphics[width=0.8\hsize,clip=true,viewport=2cm 1.5cm 12cm 7.3cm]{modelB.waypoints-gz.eps}](img29.png)
|
![\includegraphics[width=0.6\hsize]{fig/field.eps}](img30.png)
|
It was argued earlier that a cellular automata representation of space did not seem appropriate for our purposes, because of problems with off-axis movement. Instead, we use a continuous representation of space. However, some aspects of our simulation, like the calculation of forces that affect the agent, depend on the spatial location of the agent. These forces are relatively expensive to calculate, since one needs to enumerate through all possible objects that could influence a given location.
Yet, since those forces do not depend on time, they can be
pre-computed before the simulation starts. In order for this to be
successful, some coarse-graining of space is necessary. For this, we
use cells of size
![]() , and assume that all
time-independent forces are constant inside a cell. The resulting
force field (Fig. 7) becomes non-continuous in space, but
this is not a problem in practice since this only influences the
acceleration of pedestrians. That is, the acceleration contribution
from the environmental forces can jump from one time step to the next,
but since time is not continuous, this is not noticeable.
, and assume that all
time-independent forces are constant inside a cell. The resulting
force field (Fig. 7) becomes non-continuous in space, but
this is not a problem in practice since this only influences the
acceleration of pedestrians. That is, the acceleration contribution
from the environmental forces can jump from one time step to the next,
but since time is not continuous, this is not noticeable.
Precomputing the values for all cells in a hiking region of, say,
![]() , does not fit into regular computer memory. To
avoid this problem, we implemented two methods: lazy initialization,
and disk caching. By lazy initialization, we mean that the
values are computed only when an agent really needs them, also knows
as Virtual Proxy Pattern
(Gamma et al., 2001, pages 207-217).
In practice, the
simulation area is divided into blocks of size
, does not fit into regular computer memory. To
avoid this problem, we implemented two methods: lazy initialization,
and disk caching. By lazy initialization, we mean that the
values are computed only when an agent really needs them, also knows
as Virtual Proxy Pattern
(Gamma et al., 2001, pages 207-217).
In practice, the
simulation area is divided into blocks of size
![]() .
Every time an agent enters one of these blocks, the values for
all cells inside that block are computed. Since hiking paths
cross only a small fraction of those blocks, the cell values for many
blocks in our hiking area will never be calculated.
.
Every time an agent enters one of these blocks, the values for
all cells inside that block are computed. Since hiking paths
cross only a small fraction of those blocks, the cell values for many
blocks in our hiking area will never be calculated.
In addition, the cell values, once computed, are stored on disk (disk caching). Every time when an agent encounters a block for which the cell values are not in memory, the simulation first checks if they are maybe on disk. Computation of the cell values is only started when those values are not found on disk. In consequence, a simulation started for the first time will run more slowly, because the disk cache is not yet filled.
If the simulation runs out of memory, then blocks which are no longer needed, i.e. which have not been crossed by an agent for a long time, are unloaded from memory. If they are needed again, they are just re-loaded from disk. This corresponds to the Least Recently Used (LRU) Page Replacement Algorithm described by Tanenbaum (2001, pages 218-222).
An additional advantage of the blocks, well known from molecular
dynamics simulations, is that one can use them to cut off the
short-range interaction between the pedestrians. Agents which are not
in the same or one of the eight adjacent blocks are ignored. This
implies that there needs to be some data structure where agents are
registered to the block. Agents that move from one block to another
need to unregister in the first block and register in the next one.
In this way, an agent searching for its neighbors only needs to go
through the registered agents in the relevant blocks. This brings the
computation complexity from O(![]() ) down to O(
) down to O(![]() ), where
), where ![]() is the
number of all agents in the simulation, and
is the
number of all agents in the simulation, and ![]() is the number of
agents in a single block.
is the number of
agents in a single block. ![]() is a reasonably small number when
compared to the number
is a reasonably small number when
compared to the number ![]() of all agents in a real-world scenario.
of all agents in a real-world scenario.
For a testing scenario, of size
![]() , we would need
approx.
, we would need
approx.
![]() cells or
cells or ![]() blocks, resulting in
9 GByte memory requirement. The result of the lazy initialization
together with the caching mechanism is that 50 MByte are enough for
the scenario shown in Fig. 11. The computational
speed for that simulation, with 500 hikers, was about 100 times faster
than real time.
blocks, resulting in
9 GByte memory requirement. The result of the lazy initialization
together with the caching mechanism is that 50 MByte are enough for
the scenario shown in Fig. 11. The computational
speed for that simulation, with 500 hikers, was about 100 times faster
than real time.