Converting the aggregated census data

Non-equidistant bins

The size data in the 1992 U.S. economic census comes in non-equidistant bins. For example, we obtain the number of establishments with annual sales above 25000 k$, between 10000 k$ and 25000 k$, etc. For an accumulated function, such as Fig. 5 (right), this is straightforward to use. For distributions, such as Fig. 5 (left), this needs to be normalized. We have done this in the following way: (1) We first divide by the weight of each bin, which is its width. In the above example, we would divide by $(25\,000~k\$ - 10\,000~k\$) = 15\,000~k\$. Note that this immediately implies that we cannot use the data for the largest companies since we do not know where that bin ends. (2) For the log-normal distribution

$$\rho(x) \propto {1 \over x} \, \exp\big[ - ( \ln(x) - \ln(\mu) )^2 \big]$$

(note the factor $1/x$), one typically uses logarithmic bins, since then the factor $1/x$ cancels out. This corresponds to a weight of $x$ of each census data point. (3) Now we have to decide where we plot the data for a specific bin. We used the arithmic mean between the lower and the upper end. In our example case, $17\,500k\$. (4) In summary, say the number of establishments between $s_i$ and $s_{i+1}$ is $N_i$. Then the transformed number $\tilde N_i$ is calculated according to

$$\tilde N_i = {N_i \over s_{i+1} - s_i} \, {s_i + s_{i+1} \over 2} \ .$$

The largest firms

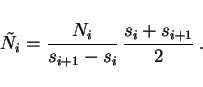
For the largest firms (but not for the large establishments), the census also gives the combined sales of the four (eight, twenty, fifty) largest firms. We used the combined sales of the four largest firms divided by four as a (bad) proxy for the sales of each of these four companies. We then substracted the sales of the four largest firms from the sales of the eight largest firms, divided again, etc. Those data points should thus be seen as an indication only, and it probably explains the ``kink'' near $2 \times 10^9$ in Fig. 5.