Spatial competition

As mentioned in the introduction, we will start with spatial models without price. We will add price dynamics later.

Basic spatial model (domain coarsening)

We use a 2-dimensional $N = L \times L$ grid with periodic boundary conditions. Sites are numbered $i=1..N$. Each site belongs to a cluster, denoted by $c(i)$. Initially, each site belongs to ``itself'', that is, $c(i) = i$, and thus cluster numbers also go from $1$ to $N$.

The dynamics is such that in each time step we randomly pick a cluster, delete it, and the corresponding sites are taken over by neighboring clusters. Since the details, in particular with respect to the time scaling, make a difference, we give a more technical version of the model. In each time step, we first select a cluster for deletion by randomly picking a number $C$ between $1$ and $N$. All sites belonging to the cluster (i.e. $c(i) = C$) are marked as ``dead''. We then let adjoining clusters grow into the ``dead'' area. Because of the interpretation later in the paper, in our model the ``dead'' sites play the active role. In parallel, they all pick randomly one of their four nearest neighbors. If that neighbor is not dead (i.e. belongs to a cluster), then the previously dead site will join that cluster. This step is repeated over and over, until no dead sites are left. Only then, time is advanced and the next cluster is selected for deletion.

In physics this is called a domain coarsening scheme (e.g. [11]): Clusters are selected and deleted, and their area is taken over by the neighbors. This happens with a total separation of time scales, that is, we do not pick another cluster for deletion before the distribution of the last deleted cluster has finished. Fig. 1 shows an example. We will call a cluster of size larger than zero ``active''.

Figure 1: Snapshot of basic domain coarsening process. LEFT: The black space comes from a cluster that has just been deleted. RIGHT: The black space is being taken over by the neighbors. -- Colors/grayscales are used to help the eye; clusters which have the same color/grayscale are still different clusters. System size $256^2$.

[width=0.4]basic-1-gz.eps [height=0.4]basic-2-gz.eps

Note that it is possible to pick a cluster that has already been deleted. In that case, nothing happens except that the clock advances by one. This implies that there are two reasonable definitions of time:

• Natural time $t$: This is the definition that we have used above. In each time step, the probability of any given cluster to be picked for deletion is a constant $1/N$, where $N = L^2$ is the system size. Note that it is possible to pick a cluster of size zero, which means that nothing happens except that time advances by one.

• Cluster time $\tilde t$: An alternative is to chose between the active clusters only. Then, in each time step, the probability of any given cluster to be picked for deletion is $1/n(\tilde t)$, where $n(\tilde t) = N - \tilde t$ is the number of remaining active clusters in the system.

Although the dynamics can be described more naturally in cluster time, we prefer natural time because it is closer to our economics interpretation.

At any particular time step, there is a typical cluster size. In fact, in cluster time, since there are $n(\tilde t) = N - \tilde t$ clusters, the average cluster size as a function of cluster time is $\overline S(\tilde t) = N / n(\tilde t) = 1 / (1 - \tilde t/N)$. However, if one averages over all time steps, we find a scaling law. In cluster time, it is numerically close to $\tilde n(s) \sim s^{-3} \hbox{ or } \tilde n(>\!s) \sim s^{-2} \ ,$ where $s$ is the cluster size, $n(s)$ is the number of clusters of size $s$, and $n(>\!s)$ is the number of clusters with size larger than $s$. In natural time, the large clusters have more weight since time moves more slowly near the end of the coarsening process. The result is again a scaling law (Fig. 2 (left)), but with exponents increased by one:

$$n(s) \sim s^{-2} \hbox{ or } n(>\!s) \sim s^{-1} \ .$$

It is important to note that this is not a steady state result. The result emerges when averaging over the whole time evolution, starting with $N$ clusters of size one and ending with one cluster of size $N$.

Figure 2: LEFT: Cluster size distribution of the basic model without injection, in natural time. Number of clusters per logarithmic bin, divided by number of clusters in first bin. The straight line has slope $-1$, corresponding to $n(s) \sim s^{-2}$ because of logarithmic bins. System size $512^2$. As explained in the text, this is not a steady state distribution, but a distribution which emerges when averaging over the complete evolution from $N$ clusters of size one to one cluster of size $N$. RIGHT: Cluster size distribution for random injection. Number of clusters per logarithmic bin, divided by number of clusters in first bin. The plot shows $p_{\it inj} = 0.01$ and system sizes $64^2$, $128^2$, $256^2$, and $512^2$. The line is a log-normal fit. This is a steady state distribution.

Random injection with space

In view of evolution, for example in economics or in biology, it is realistic to inject new small clusters. A possibility is to inject them at random positions. So in each time step, before the cluster deletion described above, in addition with probability $p_{\it inj}$ we pick one random site $i$ and inject a cluster of size one at $i$. That is, we set $c(i)$ to $i$. This is followed by the usual cluster deletion. It will be explained in more detail below what this means in terms of system-wide injection and deletion rates.

This algorithm maintains the total separation of time scales between the cluster deletion (slow time scale) and cluster growth (fast time scale). That is, no other cluster will be deleted as long as there are still ``dead'' sites in the system. Note that the definition of time in this section corresponds to natural time.

The probability that the injected cluster is really new is reduced by the probability to select a cluster that is already active. The probability of selecting an already active cluster is $n(t)/N$, where $n(t)$ is again the number of active clusters. In consequence, the effective injection rate is

$$r_{\it inj,eff} = p_{\it inj} - n(t)/N \ .$$

Similarly, the effective cluster deletion depends on the probability of picking an active cluster, which is $n(t)/N$. In consequence, the effective deletion rate is

$$r_{\it del,eff} = n(t)/N \ .$$

This means that, in the steady state, there is a balance of injection and deletion, $n_*/N = p_{\it inj} - n_* / N$, and thus the steady state average cluster number is

$$n_* = N \, p_{\it inj} / 2 \ .$$

In consequence, the steady state average cluster size is

$$s_* = N/n_* = 2 / p_{\it inj} \ .$$

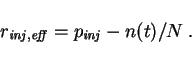
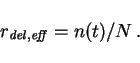
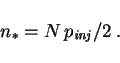
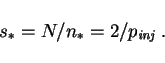
The cluster size distribution for the model of this section is numerically close to a log-normal distribution, see Fig. 2 (right). Indeed, the position of the distribution moves with $1/p_{\it inj}$ (not shown). In contrast to Sec. 3.1, this is now a steady state result.

Injection on a line

It is maybe intuitively clear that the injection mechanism of the model described in Sec. 3.2 destroys the scaling law from the basic model without injection (Sec. 3.1), since injection at random positions introduces a typical spatial scale. One injection process that actually generates steady-state scaling is injection along a 1-d line. Instead of the random injection of Sec. 3.2, we now permanently set

$$c(i) = i$$

for all sites along a line. Fig. 3 (left) shows a snapshot of this situation.

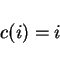
In this case, we numerically find a stationary cluster size distribution (Fig. 3 (right)) with

$$n(s) \sim s^{-1.5} \hbox{ or } n(>\!s) \sim s^{-0.5} \ .$$

Since the injection mechanism here does not depend on time, and since the cluster size distribution itself is stationary, it is independent from the specific definition of time.

Figure 3: LEFT: Injection along a line. System size $256^2$. RIGHT: Scaling plot for basic model plus injection on a line. Number of clusters per logarithmic bin, divided by number of clusters in first bin. The straight line has slope $-1/2$ corresponding to $n(s) \sim s^{-3/2}$. System size $1024^2$. This is a steady state distribution.

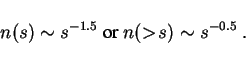
[width=0.4]snap-line-gz.eps [width=0.55]line-scaling-gpl.eps

Random injection without space

One could ask what would happen without space. A possible translation of our model into ``no space'' is: Do in parallel: Instead of picking one of your four nearest neighbors, you pick an arbitrary other agent (random neighbor approximation). If that agent is not dead, copy its cluster number. Do this over and over again in parallel, until all agents are part of a cluster again. A cluster is now no longer a spatially connected structure, but just a set of agents. In that case, we obtain again power laws for the size distribution, but this time with slopes that depend on the injection rate $p_{\it inj}$ (Fig. 4); see Sec. 4.4 for details.

Figure 4: Steady state cluster size distributions for different non-spatial simulations. Number of clusters per logarithmic bin, divided by number of clusters is first bin. System sizes $64^2$ to $512^2$. LEFT: $p_{\it inj}=0.1$. RIGHT: $p_{\it inj} = 0.01$.

[width=0.49]nsptl-p10-gpl.eps [width=0.49]nsptl-p01-gpl.eps

Real world company size distributions

Fig. 5 shows actual retail company size distributions from the 1992 U.S. economic census [12], using annual sales as a proxy for company size. We use the retail sector because we think that it is closest to our modelling assumptions -- this is discussed at the end of Sec. 6. We show two curves: establishment size, and firm size. It is clear that in order to be comparable with our model assumptions, we need to look at establishment size rather than at company size.

Census data comes in unequally spaced bins; the procedure to convert it into useable data is described in the appendix. Also, the last four data points for firm size (not for the establishment size, however) were obtained via a different method than the other data points; for details, again see the appendix.

From both plots, one can see that there is a typical establishment size around $400000 annual sales; and the typical firm size is a similar number. This number intuitively makes sense: With, say, income of 10% of sales, smaller establishments will not provide a reasonable income.

One can also see from the plots that the region around that typical size can be fitted by a log-normal. We also see, however, that for larger numbers of annual sales, such a fit is impossible since the tail is much fatter. A scaling law with

$$n(>\!s) \sim s^{-1} \hbox{\ \ corresponding to \ \ } n(s) \sim s^{-2}$$

is an alternative here.

This is, however, at odds with investigations in the literature. For example, Ref. [13] find a log-normal, and by using a Zipf plot they show that for large companies the tail is less fat than a log-normal. However, there is a huge difference between our and their data: They only use publicely traded companies, while our data refers to all companies in the census. Indeed, one finds that their plot has its maximum at annual sales of $\$10^8$, which is already in the tail of our distribution. This implies that the small scale part of their distribution comes from the fact that small companies are typically not publicely traded. In consequence, it reflects the dynamics of companies entering and exiting from the stock market, not entry and exit of the company itself.

We conclude that from available data, company size distributions are between a log-normal and a power law with $n(s) \sim s^{-2}$ or $n(>\!s) \sim s^{-1}$. Further investigation of this goes beyond the scope of this paper.

Figure 5: 1992 U.S. Economic Census data. LEFT: Number of retail establishments/retail firms per logarithmic bin as function of annual sales. RIGHT: Number of establishments/firms which have more sales than a certain number.

[width=0.49]sales-loglog-gpl.eps [width=0.49]sales-accum-gpl.eps