We are looking again at the ``basic model''. In cluster time this was: randomly pick one of the clusters, and give it to the neighbors. The following heuristic model gives insight:
At the moment, we do not have a consistent explanation for the
log-normal distribution in the spatial model. A candidate is the
following: Initially, most injected clusters of size one are
within the area of some larger and older cluster. Eventually,
that surrounding cluster gets deleted, and all the clusters of size
one spread in order to occupy the now empty space. During this phase
of fast growth, the speed of growth is proportional to the perimeter,
and thus to ![]() , where
, where ![]() is the area. Therefore,
is the area. Therefore, ![]() follows a biased multiplicative random walk, which means that
follows a biased multiplicative random walk, which means that
![]() follows a biased additive random walk.
In consequence, once that fast growth process stops,
follows a biased additive random walk.
In consequence, once that fast growth process stops, ![]() should
be normally distributed, resulting in a log-normal distribution for
should
be normally distributed, resulting in a log-normal distribution for
![]() itself. In order for this to work, one needs that this growth
stops at approximately the same time for all involved clusters. This
is apprixomately true because of the ``typical'' distance between
injection sites which is inversely proportional to the injection rate.
More work will be necessary to test or reject this hypothesis.
itself. In order for this to work, one needs that this growth
stops at approximately the same time for all involved clusters. This
is apprixomately true because of the ``typical'' distance between
injection sites which is inversely proportional to the injection rate.
More work will be necessary to test or reject this hypothesis.
If one looks at a snapshot of the 2D picture for ``injection on a
line'' (Fig. 3), one recognizes that one can
describe this as a structure of cracks which are all anchored at the
injection line. There are ![]() such cracks (some of length zero);
cracks merge with increasing distance from the injection line, but
they do not branch.
such cracks (some of length zero);
cracks merge with increasing distance from the injection line, but
they do not branch.
According to Ref. [14], this leads naturally
to a size exponent of ![]() , as found in the simulations. The
argument is the following: The whole area,
, as found in the simulations. The
argument is the following: The whole area, ![]() , is covered by
, is covered by
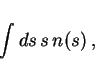
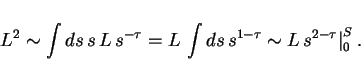
Assuming that ![]() , then the integral does not converge for
, then the integral does not converge for
![]() , and we need to take into account how the cut-off
, and we need to take into account how the cut-off ![]() scales with
scales with ![]() . This depends on how the cracks move in space as a
function of the distance from the injection line. If the cracks are
roughly straight, then the size of the largest cluster is
. This depends on how the cracks move in space as a
function of the distance from the injection line. If the cracks are
roughly straight, then the size of the largest cluster is ![]() .
If the cracks are random walks, then the size of the largest cluster
is
.
If the cracks are random walks, then the size of the largest cluster
is ![]() . In consequence:
. In consequence:
Without space, clusters do not grow via neighbors, but via random
selection of one of their members. That is, we pick a cluster, remove
it from the system, and then give its members to the other clusters
one by one. The probability that the agent choses a cluster ![]() is
proportional to that cluster's size
is
proportional to that cluster's size ![]() . If for the moment we
assume that time advances with each member which is given back, we
obtain the rate equation
. If for the moment we
assume that time advances with each member which is given back, we
obtain the rate equation
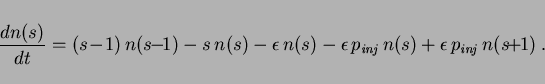
Via the typical approximations
![]() etc. we
obtain, for the steady state,
the differential equation
etc. we
obtain, for the steady state,
the differential equation
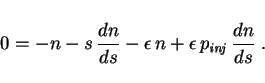
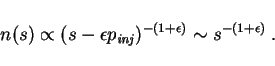
![[*]](footnote.png)