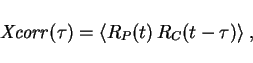Price formation

What we will do now is to add the mechanism of price formation to our spatial competition model. For this, we identify sites with consumers/customers. Clusters correspond to domains of consumers who go to the same shop/company. Intuitively, it is clear how this should work: Companies which are not competitive will go out of business, and their customers will be taken over by the remaining companies. The reduction in the number of companies is balanced by the injection of start-ups. Companies can go out of business for two reasons: losing too much money, or losing too many customers. The first corresponds to a price which is too low; the second corresponds to a price which is too high.

We model these aspects as follows: We again have $N$ sites on an $N = L \times L$ grid with periodic boundary conditions (torus). On each site, we have a consumer and a firm. These are not connected in any way except by the spatial position - one can imagine that the firm is located ``downstairs'' while the consumer lives ``upstairs''. Firms with customers are called ``active'', the other ones ``inactive''. A time step consists of the following sub-steps:

• Trades are executed.

• Companies with negative profit go out of business.

• Companies change prices.

• New companies are injected.

• Consumers can change where they shop.

These steps are described in more detail in the following:

Trade: All customers have an initial amount $M$ of money, which is completely spent in each time step and replenished in the next. Every customer $i$ also knows which firm $j=f(i)$ he/she buys from. Thus, he/she orders an amount $Q_i = M/P_j$ at his/her company, where $P_j$ is that company's price. The companies produce to order, and then trades are executed. That is, a company that has $n_j$ customers and price $P_j$ will produce and sell $Q_j = n_j M/P_j$ units and will collect $n_j M$ units of money.

Company exit: We assume an externally given cost function for production, $C(Q)$, which is the same for everybody. If profit $\Pi_j := n_j \, M - C(n_j \, M/P_j)$ is less than zero, then the company is losing money and will immediately go out of business. The prices of such a company is set to infinity. We will use $C(Q)=Q$, corresponding to a linear cost of production. With this choice, companies with prices $P_j<1$ will exit according to this rule as soon as they attract at least one customer.

Price changes: With probability one, pick a random integer number between $1$ and $N$. If there is an active company with that number, its price is randomly increased or decreased by $\delta$.

Company injection: Companies are made active by giving them one customer: With probability $p_{\it inj}$, pick a random site $i$ and make the consumer $i$ go shopping at company $i$. The price of the injected company is set to the price that the customer has paid before, randomly increased or decreased by $\delta$.

Consumer adaptation: All customers whose prices got increased (either via ``company exit'' or via ``price changes'') will search for a new shop. These ``searching'' consumers correspond to dead sites in the basic spatial models (Sec. 3), and the dynamics is essentially a translation of that: All searching consumers in parallel pick a random nearest neighbor. If that neighbor is also searching, nothing happens. If that neighbor is however not searching, and if that neighbor is paying a lower price, our consumer will accept the neighbor's shop. Otherwise the customer will remain with her old shop, and she will no longer search. We keep repeating this until no consumer is searching any more.

This model does not invest much in terms of rational or organized behavior by any of the entities. Firms change prices randomly; and they exit without warning when they lose money. New companies are injected as small variations of existing companies. Consumers only make moves when they cannot avoid it (i.e. their company went out of business and they need a new place to go shopping) or when prices just went up. Only in the last case they actively compare some prices. It will turn out (see below) that even that price comparison is not necessary.

In the above model, price converges to the unit cost of production, which is the competetive price. In Fig. 6 (left, bottom curve) we show how an initially higher price slowly decreases towards a price of one. The reason for this is that, as long as prices are larger than one, there will be companies that, via random changes or injection, have a lower price than their neighbors. Eventually, these neighbors raise prices, thus driving their customers away and to the companies with lower prices. If, however, a company lowers its price below one, then it will immediately exit after it has attracted at least one customer.

Figure 6: LEFT: Price adjustment. Bottom curve: when searching consumers compare prices. Top curve: when searching consumers accept prices no matter what they are. RIGHT: Prices tracking the cost of production.

[width=0.49]series-gpl.eps [width=0.49]track-gpl.eps

As already mentioned above, it turns out that the price comparison by the consumers is not needed at all. We can replace the rule ``if price goes up, try to find a better price'' by ``if price goes up, go to a different shop no matter what the price there''. In both cases, we find the alternative shop via our neighbors, as we have done throughout this paper. The top curve in Fig. 6 shows the resulting price adjustment. Clearly, the price still moves towards the critical value of one, but it moves more slowly and the trajectory displays more fluctuations. This is what one would expect, and we think it is typical for the situation: If we reduce the amount of ``rationality'', we get slower convergence and larger fluctuations.

In terms of cluster size distribution, the price model is similar to the earlier spatial competition model with random injection. They would become the same if we separated bankruptcy and price changes.

In Fig. 6 (right) we also show that our model is able to track slowly varying costs of production. For this, we replace $C(Q)=Q$ by a sinus-function which oscillates around $Q$. The plot implies that prices lag behind the costs of production.

Figure 7: Crosscorrelation function between $R_{\it price}$ and $R_{\it cost}$: $R_x := x(t) / x(t\!-\!1)$; ${\it Xcorr}(\tau) := \langle R_P(t) R_C(t\!-\!\tau) \rangle$. LEFT: Simulation. The crosses show the crosscorrelation values mirrored at the $\tau =0$ axis, in order to stress the asymmetry. RIGHT: U.S. Consumer price index for price and Producer price index for cost. Filled boxes are the crosscorrelation values; the smooth line is an interpolating spline for the filled boxes. The crosses show the crosscorrelation values mirrored at the $\tau =0$ axis.

[width=0.49]s-corr-gz.eps [width=0.49]f-corr-gz.eps

This is also visible in the asymmetry of the cross correlation function between both series. In order to be able to compare with non-stationary real world series, we look at relative changes, $R_x(t) = x(t) / x(t-1)$. The cross correlation function between price increases and cost increases then is

$${\it Xcorr}(\tau) = \langle R_P(t) \, R_C(t-\tau) \rangle \ ,$$

where $\langle . \rangle$ averages over all $t$. In Fig. 7 (left) one can clearly see that prices are indeed lagging behind costs for our simulations. In order to stress the asymmetry, we also plot ${\it XCorr}(-\tau)$. In Fig. 7 (right) we show the same analysis for the Consumer Price Index vs. the Production Price Index (seasonally adjusted). Although the data is much more noisy, it is also clearly asymmetric.