[[Muss das nochmal nachsehen, denn ich denke, dies ist sogar noch st"arker: es gibt nur EIN lokales min, welches damit auch das globale ist.-???]]
One of the major advantages of static assignment is that, under certain conditions, it has one unique solution. This means that no matter what the solution method, all solutions are the same. This is vastly different from our simulation approach, and certainly one of the big drawbacks of simulation that we have to consider in our work.
Sufficient conditions for uniqueness of Static Assignment are:
Strict convexity of ![]() means, intuitively, that it is
``bent'' (curved) upwards everywhere. In one dimension, this would be
ensured by having a second derivative that is
means, intuitively, that it is
``bent'' (curved) upwards everywhere. In one dimension, this would be
ensured by having a second derivative that is ![]() everywhere. In
higher dimensions, it is ensured by having a Hessian (
everywhere. In
higher dimensions, it is ensured by having a Hessian (![]() matrix of
second derivatives) that positive definite. A matrix
matrix of
second derivatives) that positive definite. A matrix ![]() is positive
definite if
is positive
definite if
![]() for all
for all
![]() -
this is just the higher dimensional version of ``second derivative
-
this is just the higher dimensional version of ``second derivative
![]() everywhere''.
everywhere''.
For an unconstrained problem, the intuitive interpretation is as
follows: Assume there is one location ![]() where
where
![]() , which is therefore a candidate for an
optimum. Now if
, which is therefore a candidate for an
optimum. Now if ![]() is curved upwards everywhere, then
candidate is a local minimum, and there cannot be a second
place where
is curved upwards everywhere, then
candidate is a local minimum, and there cannot be a second
place where
![]() .
.
For constrained optimization, one has in addition to make sure that the boundaries cooperate. This is indeed achieved by the convexity of the feasible region, see Sec. 28.5.2.
For Static Assignment, it is possible to simplify the condition of a
positive definite Hessian. The calculus for this is a bit tricky, but
workable. The result is that the statement


One has to note that the above will prove convexity of ![]() with
respect to the link flows
with
respect to the link flows ![]() , not with respect to the path flows
, not with respect to the path flows
![]() . And indeed, the solution is unique with respect to the
link flows, but not with respect to the path flows.
. And indeed, the solution is unique with respect to the
link flows, but not with respect to the path flows.
The feasible region is the set of all solutions which fulfill the constraints. That is, all path flows which fulfill the OD matrix.
Convexity of the feasible region means that any convex combination of
feasible solutions is again feasible. A convex combination is a
normalized linear combination: If ![]() and
and ![]() are both feasible,
then
are both feasible,
then
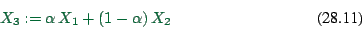 |
(28.9) |
[[intuitively, convexity would also avoid ``local optima at the boundaries'' (see Fig.). This would guarantee convergence of any hillcliming method --???]]
![]() together with
together with
![]() will always
result in a convex feasible region.
will always
result in a convex feasible region.