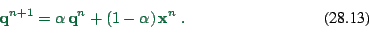Constrained optimization is a large area of mathematics, with very sophisticated techniques. Some of these techniques can be used for the static assignment problem (95).
Here we want to outline one well-known technique. It is known as Frank-Wolfe algorithm, or convex combinations method. It can be explained in a general way, and then be applied to static assignment, but it can also be applied directly to static assignment, which allows to take advantage of some simplifications right from the beginning. Here we will do the latter.
The idea is to iteratively apply three steps:
Linearize ![]() around some operating point
around some operating point ![]() ,
where
,
where ![]() denotes the iteration. That is, approximate
denotes the iteration. That is, approximate
![]() by
by
Search, on that hyperplane, for the best solution. On a plane,
the best solution is necessarily at the border, so it is sufficient to
search the border. Denote this solution by
![]() .
.
Use a convex combination of ![]() and
and ![]() for a new
solution:
for a new
solution:
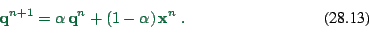
Ad Item 1: Let us calculate ![]() when applied
to
when applied
to ![]() as defined in Eq. (28.7). Let us do that
by component, i.e.
as defined in Eq. (28.7). Let us do that
by component, i.e.
![]() . This is the partial derivative with
respect to the
. This is the partial derivative with
respect to the ![]() th link flow. Only one contribution of the sum
depends on
th link flow. Only one contribution of the sum
depends on ![]() at all, and for this one the derivative is trivial:
at all, and for this one the derivative is trivial:
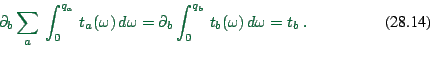
Ad Item 2: Eq. (28.15) is maybe a little
difficult to interpret at first sight, but it is actually rather
straightforward. The task is to minimize ![]() such that the
constraints are fulfilled. The constraints are that
such that the
constraints are fulfilled. The constraints are that
![]() fulfills the OD flow conditions. Note that there is no difference
if one minimizes
fulfills the OD flow conditions. Note that there is no difference
if one minimizes ![]() or
or
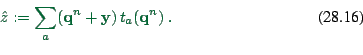
![]() just means that one has to find feasible flows
just means that one has to find feasible flows
![]() such that the sum of all link travel times is minimized,
together with the property that link travel times do not depend
on the flows. This is achieved when every flow takes the fastest
path through the network. In other words,
such that the sum of all link travel times is minimized,
together with the property that link travel times do not depend
on the flows. This is achieved when every flow takes the fastest
path through the network. In other words, ![]() is minimized
when OD flows are assigned according to fastest paths based on
the last iteration.
is minimized
when OD flows are assigned according to fastest paths based on
the last iteration.
Interpret that in terms of our agent-based approach: one finds that, given an iteration, progress is made be rerouting some of the OD flows according to what would have been fastest in the last iteration. This is exactly the same in both approaches.
Ad Item 3: The remaining task is to combine the
previous solution ![]() and the solution, let us call it
and the solution, let us call it ![]() , which minimizes
, which minimizes ![]() . As said above, this is done via a
convex combination, i.e.
. As said above, this is done via a
convex combination, i.e.