![]() choice between two options.
choice between two options.
Option ![]() , for example ``go swimming''.
, for example ``go swimming''.
Has systematic utility (that we compute): ![]() .
.
Assume that (for whatever reason) there is also a random component:
![]() Choice is made according to
Choice is made according to ![]() .
.
Possible interpretations:
Person making the choice is not determinstic.
Person making the choice is deterministic, but there are additional criteria (for example ``was swimming yesterday'') which are not included.
If they were included, then there would be no ![]() in this
interpretation.
in this
interpretation.
Now let us assume there are two options, ![]() (``go swimming'') and
(``go swimming'') and ![]() (``stay home'').
(``stay home'').
We assume that the option with the larger utility is selected (cf.
Fig. 29.1):
![\includegraphics[width=0.8\hsize]{overlap-gpl.eps}](img589.png)
|
Assume that ![]() ,
, ![]() are linear in contributions:
are linear in contributions:
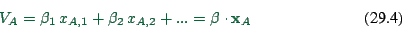 |
(29.4) |
 |
(29.5) |
In principle, the ![]() can be arbitrary functions. In practice,
they are usually simple transformations of basic variables, e.g. time, or distance, or distance squared.
can be arbitrary functions. In practice,
they are usually simple transformations of basic variables, e.g. time, or distance, or distance squared.
A result from discrete choice modeling often looks like this:
![\begin{displaymath}
\begin{tabular}{\vert c\vert c\vert c\vert}
\hline
Car & Bus...
...r[cent] & cost with bus[cent] & -0.012 \\
\hline
\end{tabular}\end{displaymath}](img594.png) |
(29.6) |
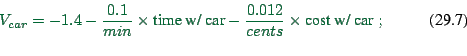 |
(29.7) |
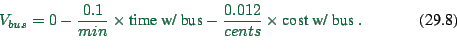 |
(29.8) |
(Compare: departure time ex.; but this here has only two options.)
For example: Time with car 10min; with bus 20min. Cost with car
200cents; with bus 100cents. Then
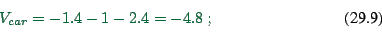 |
(29.9) |
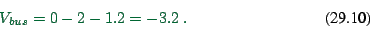 |
(29.10) |
The probas to select car/bus (see later) will be something like
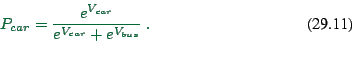 |
(29.11) |
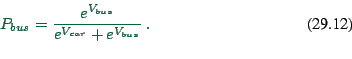 |
(29.12) |
| Car | Bus | Coeff |
| 1 | 0 | -1.4 |
| time with car[min] | time with bus[min] | -0.1 |
| cost with car[cent] | cost with bus[cent] | -0.012 |
| 1 if female | 0 | 0.6 |
| 1 if ( unmarried OR spouse cannot drive OR travels to work w/ spouse ) | 0 | -0.2 |
| 1 if ( married AND spouse is working AND spouse drives to work indep'y ) | 0 | 1.2 |
Meanings:
If person is female, utility of car is increased.
If person is unmarried OR if spouse cannot drive OR if person travels to work with spouse, then utility of car is decreased.
Etc.
From this point on, progress is made by making assumptions about the
statistical distributions of the noise parameters ![]() . Different
assumptions will lead to different models.
. Different
assumptions will lead to different models.
Before looking into some specific forms, it makes sense to quickly recall probability distributions and generating functions.
A probability density function essentially gives the probability
that a certain option is selected. For example, the Gaussian
probability density function
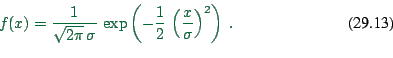 |
(29.13) |

The generating function ![]() is the integral of the
probability density function. That is
is the integral of the
probability density function. That is

The generating function can be used to compute the probability that
the selected value is smaller than some given value ![]() . Rather
obviously, one has
. Rather
obviously, one has
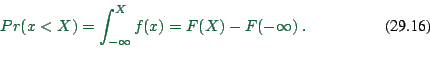
Recall: We have
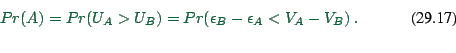 |
(29.14) |
We are now looking for mathematical forms of ![]() .
.
Assume that ![]() and
and ![]() are Gaussian distributed.
are Gaussian distributed.
Gaussian distributions have the property that sums/differences of
Gaussian distributed variables are still Gaussian distributed. In
consequence,
![]() is Gaussian
distributed, for example (with mean zero and ``width''
is Gaussian
distributed, for example (with mean zero and ``width'' ![]() ):
):
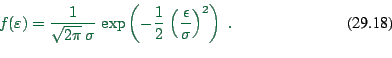 |
(29.15) |
![\includegraphics[height=0.4\hsize,width=0.6\hsize]{gz/gauss.eps.gz}](img616.png) [[
[[![\includegraphics[height=0.4\hsize,width=0.6\hsize]{erf-gpl.eps}](img615.png) ]] ]]
|
Now we need
![]() , where
, where
![]() , and we know that
, and we know that
![]() is normally distributed. As equation:
is normally distributed. As equation:
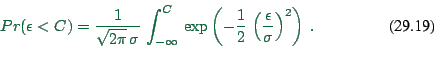 |
(29.16) |
The solution of this needs the so-called error function, sometimes denoted by erf, or double erf(double x) under linux. Before the age of electronic computers, the error function was inconvenient to use, which is why the main theoretical development followed a different path, described in the following.
An important piece of knowledge is what happens when random variables are combined. For example, the sum of two Gaussian-distributed random variables are again Gaussian-distributed.
As preparation, learn about the so-called Gumbel distribution:
Generating function
![\begin{displaymath}
F(\epsilon) = \exp[ - e^{ - \mu \, (\epsilon - \eta) } ] \ .
\end{displaymath}](img620.png) |
(29.17) |
Probability denstity function
![\begin{displaymath}
f(\epsilon) = F'(\epsilon) = \mu \, e^{- \mu \, (\epsilon - \eta)}
\, \exp[ - e^{- \mu \, (\epsilon - \eta)} ] \ .
\end{displaymath}](img621.png) |
(29.18) |
Location of maximum: ![]() (location parameter).
(location parameter).
Variance:
![]() (
(![]() width
parameter).
width
parameter).
(Remember: Sum of two Gaussian rnd variables ![]() new Gaussian
rnd variable with properties ...)
new Gaussian
rnd variable with properties ...)
For Gumbel:
If ![]() and
and ![]() indep Gumbel with same
indep Gumbel with same ![]() , then
, then
![]() also Gumbel-distributed with the same
also Gumbel-distributed with the same ![]() and a new
and a new ![]() of
of
![\begin{displaymath}
\mu^{-1} \, \ln[ e^{\mu \eta_1} + e^{\mu \eta_2} ] \ .
\end{displaymath}](img627.png) |
(29.19) |
If ![]() and
and ![]() indep Gumbel with same
indep Gumbel with same ![]() ,
then
,
then
![]() is logistically distributed
(see below) with generating function
is logistically distributed
(see below) with generating function
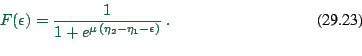 |
(29.20) |
Generating
function:
![]() Note that
Note that
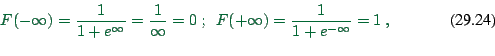 |
(29.21) |
Probability density function:
![]() The logistic probability density function looks somewhat similar to
the Gaussian probability density function
(Fig. 29.3).
The logistic probability density function looks somewhat similar to
the Gaussian probability density function
(Fig. 29.3). ![]() is the width parameter.
is the width parameter.
![\includegraphics[width=0.6\hsize]{logistic-vs-gauss-gpl.eps}](img633.png)
![\includegraphics[width=0.6\hsize]{logistic-vs-gauss-logscale-gpl.eps}](img634.png)
|
Coming back to binary choice, one now assumes that ![]() and
and
![]() are Gumbel distributed, meaning that
are Gumbel distributed, meaning that
![]() is logistically distributed.
is logistically distributed.
Again, find
![]() . This is
. This is
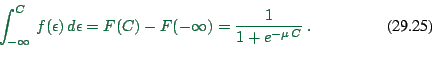 |
(29.22) |
If we re-translate this into our original variables, we obtain
![]()
This is similar to what we have seen in the departure time choice (except that here are only two options; for departure time choice we had many).
Note that the noise parameter ![]() comes from the width parameter of
the logistic distribution. Large noise
comes from the width parameter of
the logistic distribution. Large noise ![]() small
small ![]() (
(![]() small
inverse temperature)
small
inverse temperature) ![]() choice more random.
choice more random.