Multinomial choice

Now more than two choices, e.g.:

Go swimming, go shopping, stay home, go to movies, ...

Many possible times-to-depart (discretized into 5-min bins).

See Fig. 29.4.

Figure 29.4: Multiple probability density functions for different options. If one picks $U_A$ and $U_B$, then the probability that C is selected is given by the probability that $U_C$ is larger than the maximum of $U_A$ and $U_B$.

Concentrate on option ``1''.

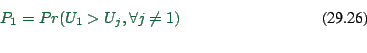$$P_1 = Pr(U_1 > U_j, \forall j \ne 1)$$ (29.23)

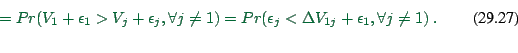$$= Pr( V_1 + \epsilon_1 > V_j + \epsilon_j, \forall j \ne 1) ... ... \epsilon_j < \Delta V_{1j} + \epsilon_1, \forall j \ne 1) \ .$$ (29.24)

Alternatively:

$$P_1 = Pr\left[ \epsilon_1 > \max_{j \ne 1}[ \Delta V_{1j} + \epsilon_j ] \right] \ .$$ (29.25)

This is similar to binary choice, i.e. Eq. (29.3). In binary choice, progress was made by assuming that the $\eps_i$ were either Gaussian or Gumbel distributed. The same will happen here.

As in binary choice, a Gaussian distribution will lead to use of the error function. This will not be discussed any further here.

A Gumbel distribution will lead to the use of the logistic distribution.

Multinomial logit (MNL)

$=$ multinomial choice with Gumbel-distributed randomness.

We had:

$$P_1 = Pr\left[ \epsilon_1 > \max_{j \ne 1}[ \Delta V_{1j} + \epsilon_j ] \right] \ .$$ (29.26)

Two steps:

$\epsilon_j \ (j \ne 1)$ Gumbel-distributed

$\Rightarrow$ $\epsilon_* := \max_{j \ne 1}[ \Delta V_{1j} + \epsilon_j ]$ also Gumbel-distributed.

$\epsilon_1$ and $\epsilon_*$ Gumbel-distributed

$\Rightarrow$ $\epsilon_* - \epsilon_1$ logistically distributed.

Only problem is to keep track of the transformations of the two parameters $\eta$ and $\mu$.

Result of second step is (remember: similar to binary logit)

Either via normalization or via really computing $V_*$ as the new $\eta$ of the Gumbel distribution one obtains