Our approach

The approach that is maybe closest to our work are the discrete choice models (Ben-Akiva and Lerman, 1985). As is well known, in that approach the utility $V_i$ of an alternative $i$ is assumed to have a systematic component $U_i$ and a random component $\eta_i$. Under certain assumptions for the random component this implies that the probability $p_i$ (called choice function) to select alternative $i$ is

$$p_i = \exp(\beta U_i) / \sum_k \exp(\beta U_k) \ .$$ (36.1)

$p_i$ could for example represent the probability to accept a workplace that is $i$ seconds away. If $i$ is indeed taken as time, then $U_i$ is negative, and it follows an inverse S-shaped curve which starts at zero, decreases slowly for small times, decreases faster for medium times, and decreases again slowly for large times (Bowman, 1998). By this approach, our above location choice problem would be solved by weighting each given workplace according to time-distance $i$ by $p_i$ and then making a random draw in these probabilities. Clearly, for the discrete choice approach one needs to know the function $\beta U_i$.

In this paper, the ``psychological'' function $\beta U_i$ is obtained from ``observed'' trip time distributions, using new methods of micro-simulating large geographical regions. The core idea is that an observed trip time distribution $N_{tr}(t)$ can be decomposed into an accessibility part $N_{acs}(t)$ and an acceptance ($=$ choice) function $f_{ch}(t)$

$$N_{tr}(t) = N_{acs}(t) \, f_{ch}(t) \ .$$ (36.2)

$N_{acs}(t)$ is the number of workplaces at time-distance $t$; $f_{ch}(t)$ is proportional to the probability that a prospective worker will accept this trip time. Thus, apart from normalization $f_{ch}$ is the same as the choice function in discrete choice theory. Our decomposition allows to separate the network specific accessibility distribution $N_{acs}(t)$ from the ``psychological'' trip time acceptance function. In principle, $f_{ch}(t)$ as found via our relaxation method should be the same as when obtained via an estimation of a survey when suitably averaged over the whole population.

Given a micro-simulation of traffic, $N_{acs}(t)$ can be derived from the simulation result. For a given home location (and a given assumed starting time), one can build a tree of time-dependent shortest paths, and every time one encounters a workplace at time-diestance $t$, one adds that to the count for trip time $t$. The challenge is that this result depends on the traffic: Given the same geographic distribution of workplaces, these are farther away in terms of trip time when the network is congested than when it is empty. That is, given the function $f_{ch}(t)$, one can obtain the function $N_{acs}(t)$ via micro-simulation, i.e. $N_{acs}(t) = G[f_{ch}(.)](t)$, where $G$ is the micro-simulation which can be seen as a functional operating on the whole function $f_{ch}(.)$. The problem then is to find the macroscopic (i.e., averaged over all trips) function $f_{ch}(.)$ self-consistently such that, for all travel times $t$,

$$N_{tr}(t) = G[f_{ch}(.)](t) \, f_{ch}(t).$$ (36.3)

For this, a relaxation technique is used. It starts with a guess for $f_{ch}(t)$ and from there generates $N_{acs}(t) = G[f_{ch}](t)$ via simulation. A new guess for $f_{ch}(t)$ is then obtained via

$$f_{ch}^{(n+1)}(t) = N_{tr}(t) / N_{acs}^{(n)}(t) \ .$$ (36.4)

A fraction $f_{act}$ of all travelers will do their workplace selection again, using the new $f_{ch}^{(n+1)}$. $G[.]$ is generated again via micro-simulation, and this is done over and over again until a sufficiently self-consistent solution for $f_{ch}(t)$ is found.

Real census data is used for $N_{tr}(t)$ (see ``census-100''-curve in Fig. 36.3; from now on denoted as $N_{cns}(t)$). People usually give their trip times in minute-bins as the highest resolution. Since our simulation is driven by one-second time steps we need to smooth the data in order to get a continuous function instead of the minute-histogram. Many possibilities for smoothing exist; one of them is the beta-distribution approach in Wagner and Nagel (1999). Here, we encountered problems with that particular fit for small trip times: Since that fit grows out of zero very quickly, the division $N_{tr}/N_{acs}$ had a tendency to result in unrealistically large values for very small trip times. We therefore used a piecewise linear fit with the following properties: (i) For trip time zero, it starts at zero. (ii) At trip times 2.5 min, 7.5 min, 12.5 min, etc. every five minutes, the area under the fitted function corresponds to the number of trips shorter than this time according to the census data.

Obtaining $G[f_{ch}]$ itself via simulation is by no means trivial. It is now possible to micro-simulate large metropolitan regions in faster than real time, where ``micro''-simulation means that each traveler is represented individually. The model used here is a simple queuing type traffic flow model described in Simon and Nagel (1999). However, even if one knows the origins (home locations) and destinations (workplaces), one still needs to find the routes that each individual takes. This ``route assignment'' is typically done via another iterative relaxation, where, with location choice fixed, each individual attempts to find faster routes to work. Rickert (1998) and Nagel and Barrett (1997) give more detailed information about the route-relaxation procedure; see also Fig. 36.1 and its explanation later in the text.

Once $f_{ch}^{(n+1)}(t) = N_{cns}(t) / N_{acs}^{(n)}(t)$ is given, the workplace assignment procedure works as follows: The workers are assigned in random order. For each employee the time distances $t$ for all possible household/workplace pairs [hw] are calculated, while the home location $h$ is fixed and taken directly from the household data for each employee. Let $t_{hw}$ be the resulting trip time for one particular [hw] and $n_{wo}(w)$ the number of working opportunities at workplace $w$. Then, an employee in household $h$ is assigned to a working opportunity at place $w$ with probability

$$p_{hw} \propto n_{wo}(w) f_{ch}(t_{hw}).$$ (36.5)

In addition to work location, home-to-work activity information also includes the times when employees start their trip to work. These are directly taken from the household data.

The complete approach works as follows:

(1) Synthetic population generation: First a synthetic population was generated based on demographic data (Beckman et al, 1996). The population data comprises microscopic information on each individual in the study area like home location, age, income, and family status.

(2) Compute the acceptance function $f_{ch}(T)$. This is done as follows:

(2.1) For each worker $i$, compute the fastest path tree from his/her home location. Compute the resulting workplace distribution $N_{wp}(i,T)$ as a function of trip time $T$.^36.2

(2.2) Average over all these workplace distributions, i.e.

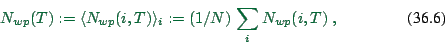$$N_{wp}(T) := \langle N_{wp}(i,T) \rangle_i := (1/N) \, \sum_i N_{wp}(i,T) \ ,$$ (36.6)

where $N$ is the number of workers, which is by definition also equal to the number of workplaces. $N_{wp}(T)$ is thus equivalent to our earlier $N_{acs}(T)$.

(2.3) Compute the resulting average choice function via

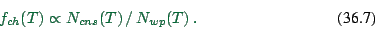$$f_{ch}(T) \propto N_{cns}(T) \, / \, N_{wp}(T) \ .$$ (36.7)

In addition, a normalization constant needs to be computed such that

$$\sum_T f_{ch}(T) = 1 \ .$$ (36.8)

(3) Assign workplaces. For each worker $i$ do:

(3.1) Compute the congestion-dependent fastest path tree for the worker's home location.

(3.2) As a result, one has for each workplace the expected trip time $T$. Counting all workplaces at trip time $T$ results in the individual accessibility distribution $N_{acs}(i,T)$.

(3.3) Randomly draw a desired trip time $T^*$ from the distribution $N_{acs}(i,T) \, f_{ch}(T)$.

(3.4) Randomly select one of the workplaces which corresponds to $T^*$. (There has to be at least one because of (3.1).)

(4) Route assignment: Once people are assigned to workplaces, the simulation is run several times (5 times for the simulation runs presented in the paper) while people are allowed to change their routes (fastest routes under the traffic conditions from the last iteration) as their workplaces remain unchanged.

(5) Then, people are reassigned to workplaces, based on the traffic conditions from the last route iteration. That is, go back to (2).

This sequence, workplace reassignment followed by several re-routing runs, is repeated until the macroscopic traffic patterns remain constant (within random fluctuations) in consecutive simulation runs. For this, one looks at the sum of all people's trip times in the simulation. The simulation is considered relaxed when this overall trip time has leveled out.

Running this on a 250 MHz SUN UltraSparc architecture takes less than one hour computational time for one iteration including activity generation, route planning, and running the traffic simulator. The 70 iterations necessary for each series thus take about 4 days of continuous computing time on a single CPU.

Figure 36.1: Iterative Activity Re-Assignment: Schematic subsequent application of activity generator, router, and traffic simulator.