
Nächste Seite: Input Data and Scenarios
Aufwärts: ersa2002
Vorherige Seite: Introduction
Unterabschnitte
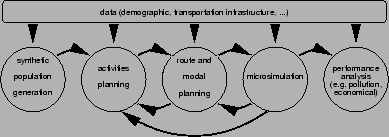
Simulation Modules
Traffic simulations for transportation planning typically consist of
the following modules (Fig. 1):
- Population generation. Demographic data is
disaggregated so that one obtains individual households and
individual household members, with certain characteristics, such
as a street address, car ownership, or household
income (Beckman et al., 1996). - This module is not used for our
current investigations but will be used in future.
- Activities generation. For each individual, a set of
activities (home, going shopping, going to work, etc.) and
activity locations for a day is
generated (Vaughn et al., 1997; Bowman, 1998). - This module is
not used in our current investigations but will be used in future.
- Modal and route choice. For each individual, the
modes are selected and routes are generated that connect activities
at different locations (see Sec. 2.1).
- Traffic micro-simulation. Up to here, all individuals
have made plans about their behavior. The traffic
micro-simulation executes all those plans simultaneously (see
Sec. 2.2). In particular, we now obtain the result of
interactions between the plans - for example congestion.
- Feedback. In addition, such an approach needs to make
the modules consistent with each other (Sec. 2.3).
For example, plans depend on congestion, but congestion depends on
plans. A widely accepted method to resolve this is systematic
relaxation - that is, make preliminary plans, run the traffic
micro-simulation, adapt the plans, run the traffic micro-simulation
again, etc., until consistency between modules is reached. The
method is somewhat similar to the Frank-Wolfe-algorithm in static
assignment, or in more general terms to a standard relaxation
technique in numerical analysis.
This modularization has in fact been used for a long time; the main
difference is that it is now feasible to make all modules completely
microscopic, i.e. each traveler is individually represented in all
modules.
Abbildung 1:
TRANSIMS modules
|
|
Routing
Travelers/vehicles need to compute the sequence of links that they are
taking through the network. A typical way to obtain such paths is to
use a shortest path Dijkstra algorithm. This algorithm uses as input
the individual link travel times plus the starting and ending point of
a trip, and generates as output the fastest path.
It is relatively straightforward to make the costs (link travel times)
time dependent, meaning that the algorithm can include the effect that
congestion is time-dependent: Trips starting at one time of the day
will encounter different delay patterns than trips starting at another
time of the day. Link travel times are fed back from the
micro-simulation in 15-min time bins, and the router finds the fastest
route based on these 15-min time bins. Apart from relatively small
and essential technical details, the implementation of such an
algorithm is straightforward (Jacob et al., 1999). It is possible
to include public transportation into the
routing (Barrett et al., 1997); in our current work, we
look at car traffic only.
Micro-Simulation
Our main micro-simulation is the queue
simulation (Cetin and Nagel, in preparation; Gawron, 1998). The intent with this
simulation is to keep travelers/vehicles microscopic and to have queue
spillback, but apart from this to keep the simulation as simple as
possible. This is similar in spirit to traffic simulations based on
the smooth particle hydrodynamics approach, such as DYNEMO
(Schwerdtfeger, 1987), DYNAMIT (its.mit.edu), or DYNASMART (Mahmassani et al., 1995).
In the queue simulation, streets are essentially represented as FIFO
(first-in first-out) queues, with the additional restrictions that (1)
vehicles have to remain for a certain time on the link, corresponding
to free speed travel time; and that (2) there is a link storage
capacity and once that is exhausted, no more vehicles can enter the
link.
A major advantage of the queue simulation, besides its simplicity, is
that it can run directly off the data typically available for
transportation planning purposes. This is no longer true for more
realistic micro-simulation, which need, for example, the number of
lanes including pocket and weaving lanes, turn connectivities across
intersections, or signal schedules.
Feedback
As mentioned above, plans (such as routes) and congestion need to be
made consistent. This is achieved via a relaxation technique
(Bottom, 2000; Kaufman et al., 1991; Nagel, 1994/95):
- Initially, the system generates a set of routes based on
free speed travel times.
- The new routes are stored in a database, called the ``agent
database'' (Raney and Nagel, 2002), so that the travelers
(``agents'') may later associate the performance of the route to
it, and may choose routes based on performance.
- The traffic simulation is run with these routes.
- Each agent measures the performance of his/her route based on
the outcome of the simulation. ``Performance'' at present means the
total travel time of the entire trip, with lower travel times
meaning better performance. This information is stored for all the
agents in the agent database, along with the route that was used.
- 10% of the population requests new routes from the router,
which bases them on the updated link travel times from the last
traffic simulation. The new routes are then stored in the agent
database.
- Travelers who did not request new routes choose a previously
tried route from the agent database by comparing performance values
for the different routes. Specifically, they use a multinomial
logit model
for the probability 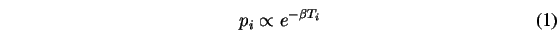 to select route
to select route 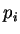 , where
, where 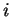 is the
corresponding memorized travel time.
is the
corresponding memorized travel time. 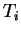 was set heuristically to
was set heuristically to
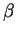 to obtain a fraction of about 10% non-optimal
users.
to obtain a fraction of about 10% non-optimal
users.
- This cycle (i.e. steps (3) through (6)) is run for 50 times;
earlier investigations have shown that this is more than enough to
reach relaxation (Rickert, 1998).
Note that this implies that routes are fixed during the traffic
simulation and can only be changed between iterations. Work is
under way to improve this situation, i.e. to allow online
re-planning (Gloor, 2001).


Nächste Seite: Input Data and Scenarios
Aufwärts: ersa2002
Vorherige Seite: Introduction
Kai Nagel
2002-05-31