

Next: Results
Up: An Improved Framework for
Previous: Implementation of the framework
Subsections
Verification setup
In order to test our implementation, verification scenarios were
designed. Those scenarios are constructed in a way that they test the
most important features of the framework. The features that are
tested are: (i) capability to relax to an approximate equilibrium
solution; (ii) capability to cooperate with more than one external
module; (iii) capability to generate a meaningful solution even with
an external module that just performs small random changes
(``mutations'') of existing plans.
A scenario consists of: (i) the network; (ii) the initial plans file;
(iii) specific implementation details. These will be treated one by
one in this section.
The network
The network used for this scenario can be seen in
Fig. 5. It consists of a circular arrangement where
in one part travelers have multiple route options. Internally, all
those routes have the same lengths and capacities, so that there is no
bias toward one or the other. The expectation is that in the relaxed
states all those routes are used equally. All roads are
uni-directional; travelers need to follow the roads clockwise.
Figure 5:
Diagram of the testing network overlaid onto example snapshots of the
Routes Only scenario at 06:08 AM, (a) before and (b) after many
iterations of route replanning. After replanning, the agents
have spread onto the different available routes between home and
work.
Link capacities are 36,000 veh/h except where indicated (the
nine route options are identical).
|
[Before replanning]
10#6
[After replanning]
11#7
|
The initial plans file
All scenarios need to start with an initial condition. In our case,
we take as initial condition a plans file which contains 2'000
agents, and one fully specified plan per agent. Those plans are the
same for all agents: They specify that the agents leave the ``Home''
location at 6:00 AM, take the middle road (through node 7) to the
``Work'' location, and work for eight hours. Then they take the lower
part of the ``circle,'' through nodes 14, 15, and 1, to return home.
The total free-speed travel time is about 54 min, with 15 min for the
trip from ``Home'' to ``Work'', and 39 min for the return trip.
The mobility simulation
As the
mobility simulation
we use an improved version of a
so-called ``queue simulation'' (17). The improvements
include an implementation on parallel computers, and an improved
intersection dynamics, which ensures a fair sharing of the
intersection capacity among incoming traffic
streams (9). As pointed out elsewhere, the
mobility simulation
takes a plans file, executes it, and returns
events information, such as when agents leave from or arrive at
activities, or when agents enter/leave links.
Agent Database
As discussed elsewhere, the agent database contains all plans for all
agents, and manages addition, modification, removal, and selection of plans.
The precise functioning of the agent database for our test scenario is
as follows:
- The agent database may be required to limit the number of plans
stored per agent to 12#8. If any agent ends up with more than
plans 12#8 plans, it continues to delete the plan with the
worst score until the number of plans is small enough.
Note that in the steps following this one, an agent may obtain a new
plan, which means it will have 13#9 plans while trying a new
one out, but it will have only 12#8 to choose from when
selecting from old plans.
- With probability 14#10, agents are selected to undergo
times replanning. Each of these agents selects an existing plan from
memory with uniform probability (not based on score) to use as a
template for the new plan. This template is immediately copied into
the agent's memory, to serve as a placeholder for the eventual new
plan. The selected plans are written to a file, and the time
replanner (see below) is called with this file as input. It writes
the resulting new plans to a separate file. The agent database reads
this file and overwrites the template in each agent's memory with the
corresponding plan from the file.
- With probability 15#11, agents are selected to undergo
route replanning. As with times replanning, each of these agents
selects an existing plan as a template and copies it into its memory
as a placeholder for the new plan.
In addition, we set the router to be dependent on the times generated
by the times replanning module, since the new leg departure times may
offer better routes than the ones currently used. Therefore, all
agents that underwent times replanning select their new plans for
route replanning as well. Note that no plans are copied for these
agents, since the plan with the new times already serves as the
template for the new routes, and overwriting it will not change the
new time information.
All the template plans are written to a single file, the route
replanner (see below) is called, the resulting new plans are written
again to file, and the agent database reads those plans and overwrites
the template plans with the new ones.
- For each agent that has multiple plans, the plan to be executed
in the following mobility simulation is selected.
- All agents that possess a new plan select that new
plan.
- A fraction 16#12 chooses a plan at random from their memory,
using a uniform probability for each plan, and ignoring plan
performance. This is done to force agents to re-evaluate existing
plans from time to time, even plans with a bad score.
- All other agents select between existing plans, with probability
17#13
where 18#14 is the score of plan 19#15 and 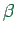 is a constant (see
below). This is just a standard multinomial logit model
(e.g. 5).
is a constant (see
below). This is just a standard multinomial logit model
(e.g. 5).
The value of 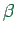 affects how likely agents choose ``non-best''
plans. Higher values of
affects how likely agents choose ``non-best''
plans. Higher values of 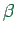 lead toward the best plan being
chosen more often, while smaller values provide a more randomized
choice. Since
lead toward the best plan being
chosen more often, while smaller values provide a more randomized
choice. Since 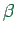 interacts with the scaling of the scoring
function, it is discussed in more detail there.
interacts with the scaling of the scoring
function, it is discussed in more detail there.
- The selected plans are written to file; the mobility simulation
runs with these plans and writes events information to a file.
- The agent database reads the resulting events, computes
corresponding scores for each agent, and adds those scores to the
existing scores according to
20#16
where 18#14 is the stored score for plan 19#15, 21#17 is the newly
calculated score, and
22#18 is a blending factor.
This leaves the question of how plans are scored that have not been
used before. Plans from the initial plan set have no history, so there
is no way to estimate their scores. Upon their first use, the agent
simply gives it the new score:
23#19
However, when plans are copied as templates for replanning, score
information is available from other plans, which can be used to
provide an estimate the initial value of 18#14. This estimate can be
calculated in many ways; at present we set it to the score of the best
plan in the agent's memory.
For this paper, we set the above parameters to the following values:
- The maximum number of plans per agent, 12#8, is 6.
- The probability of an agent to perform time replanning,
14#10, and route replanning, 15#11, are both 0.1.
- The probability of choosing a random plan, 16#12, is 0.1.
- The plan selection constant,
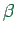 , is 2/.
Section 5.4 describes what happens when we try different
values of
, is 2/.
Section 5.4 describes what happens when we try different
values of 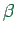 .
.
- The score blending factor, 24#20, is 0.1.
Routing module
An agent's plan must connect successive activities at different
locations by travel legs that use the transportation network. Legs
are described by their mode and mode-specific information. For
example, a car-mode leg contains a node-by-node description of the
vehicle's route through the network from the location of the previous
activity to the location of the next activity. In principle legs can
be selected from different mode types, but at present we only model
car trips. The legs have (expected) starting times, and the router
needs to be sensitive to congestion so that it can avoid using already
congested links.
We currently use a router based on Dijkstra's shortest-path algorithm,
but ``shortness'' is measured by the time it takes an agent to drive
the route rather than distance. The fastest path depends on the
travel times of each individual link (road segment) traversed in the
route. These times depend on how congested the links are, and so they
change throughout the day. This is implemented in the following way:
The way a Dijkstra algorithm searches a shortest path can be
interpreted as expanding, from the starting point of the leg, a
network-oriented version of a wave front. In order to make the
algorithm time-dependent, the speed of this wave front along a link is
made to depend on when this wave front enters the
link (e.g. 23).
That is, for each link 25#21 we need a function 26#22 which returns
the link ``cost'' (27#23 link travel time) for a vehicle entering at
time 28#24. This information is calculated from the events taken from a
run of the
mobility
simulation. In order to make the look-up of
26#22 reasonably fast, we aggregate over 15 min bins, during which
the cost function is kept constant. That is, all vehicles entering a
link between e.g. 9 AM and 9:15 AM will contribute to the average link
travel time during that time period.
Time choice module (Time mutator)
In general, we want as a second module one that generates (or modifies)
agents' activity schedules, which form the basis of their
plans (37,7). One can divide the task
of creating an activity schedule into three parts: pattern choice,
location choice, and timing choice.
The pattern choice determines which activities to perform
during the day, and in what order. For example, an agent might decide
whether or not to go shopping, and if so, before or after work.
The location choice determines where the agent will perform
each activity. For some activities, such as home and work, agents
make this decision very infrequently, while for other activities, such
as shopping, the agent might choose a different location each time it
wants to perform the activity. For example, an agent could go
shopping at a bakery close to home or a grocery store near work.
The time choice determines the duration of each activity,
including when to leave home at the start of the day.
A single module can make all of these decisions at the same time, or
separate modules can be used to handle each one individually.
For this particular study, there is only a time choice module. This
module takes the existing times of the plan and modifies them randomly.
Note that there is no ``goal'' with this module, that is, the module
does not try to improve any kind of score. Rather, the module
makes a random modification, and the plans selection mechanism in
conjunction with the scoring will make the agents improve toward
better scores.
The exact details of the time mutator are as follows.
This module reads the plans file, and for each plan alters the end
time of the first activity by a random amount 29#25 uniformly selected
in the range
30#26. Values that come before 00:00
are reset to that time. It then alters the duration of each activity
except the first and last by separate random values uniformly selected
from the same range. The last activity does not need modification
since it runs from whenever the agent arrives until 24:00. The
modified plans are written back out to a file.
Scoring
The utility function we currently use
is described in detail in Charypar and Nagel (10). For the convenience of the
reader, we summarize it here, though it is sufficient to recognize
that performing activities is rewarded, and travel, early arrival,
and late arrival are punished.
The utility function essentially translates the layout of the plan
into a numerical value, which can be thought of as a score or an
actual value in monetary terms.
Agents have a preferred duration for each activity, called the optimal
duration, and represented by 31#27. The utility for performing an
activity (
32#28) is a logarithmic function of the duration
of time spent performing the activity. It is calibrated so that
performing the activity for exactly 31#27 hours causes the
marginal utility to equal a fixed value,
33#29, which is
the same for all activity types. In addition, it sets the utility for
performing an activity for exactly 31#27 hours to be
34#30. Mathematically,
35#31
The result of the log function is that staying longer than 31#27
always gains more utility, but each additional hour gains less utility
than the preceding hour.
Charypar and Nagel (10) sets
33#29 to +20/h, though
for this study we set it to +6/h. The reason for this change is
explained below.
As mentioned previously, we have only two types of activities: home
and work.
The preferred duration of work time is 8 hours, and the preferred
duration of staying home is 16 hours, so that the agents have no free
time; i.e. their day is ``full.''
In addition to duration, we set the useful hours for performing the
work activity to between 7:00 AM and midnight, with the desired
starting time to be exactly the opening time of 7:00 AM. The home
activity has no time constraints.
The utility of an agent who arrives to work before 7:00 AM must wait
until 7:00 to start working. While waiting, the agent suffers a
penalty defined by the marginal utility of waiting, 36#32,
times the number of hours the agent waits, 37#33.
Agents arriving after 7:00 AM are assessed a lateness penalty,
determined by the marginal utility of being late, 38#34,
times the number of hours the agent is late, 39#35.
The final component of the utility is the utility of travel, which is
the marginal utility of travel,
 , times the number of
hours the agent spends traveling, 40#36.
We set the above parameters to the following values:
36#32 = 0/h;
, times the number of
hours the agent spends traveling, 40#36.
We set the above parameters to the following values:
36#32 = 0/h;
 = -6/h;
38#34 = -18/h.
= -6/h;
38#34 = -18/h.
Given a full day plan, the agent prefers to spend all 24 hours in the
day performing some activity. Any time spent by the agent not
performing an activity causes a loss of potential utility. The agent
would obtain a perfect score if it spent exactly 8 hours at work and
16 hours at home, allowing it to earn utility every minute of the day.
This would earn the agent 60 for each activity, for a total score
of 120.
In an actual day, the agent must spend some of its time traveling.
While traveling, the agent does not earn any utility for being at work
or at home, and is simultaneously losing utility for being on the
road. This means the agent incurs a double penalty: the actual
negative utility for the travel itself, and the loss of potential
positive utility for not performing an activity.
Similarly, if the agent arrives early to work, it is also not spending
time working (or being at home) so it loses potential utility. Note
that being late has a real penalty, but does not cause any loss of
potential utility, since the agent begins performing the activity
immediately upon arrival.
Therefore, there is an indirect penalty associated with arriving early
to a location (waiting) and traveling. If the agent's activity
durations are near the optimum, this penalty is approx.
41#37 times the number of hours spent waiting and/or
traveling. Since agents will do their best to allocate time to the
activities, we can assume that the durations are as near to optimum as
possible. Given that the total travel time is on the order of 1 h,
this is a reasonable assumption.
Thus, the effective values of the above parameters are approximately:
36#32 = -6/h;
 = -12/h;
38#34 = -18/h.
These effective values are selected such that, in rough terms, they
model the Vickrey model of time choice
(e.g. 2).
The desire to match the Vickrey model explains our choice of +6/h
for
33#29; if it was +20/h, the effective penalty for
arriving early would be of greater magnitude than the penalty for
arriving late.
= -12/h;
38#34 = -18/h.
These effective values are selected such that, in rough terms, they
model the Vickrey model of time choice
(e.g. 2).
The desire to match the Vickrey model explains our choice of +6/h
for
33#29; if it was +20/h, the effective penalty for
arriving early would be of greater magnitude than the penalty for
arriving late.
As mentioned earlier, the 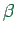 value used by the agent database to
multiply agents' scores affects their selection of those plans. This
value can be considered to be a scaling function, which maps utility
in Euro to unit-less values for the logit selection. In real-world
applications,
value used by the agent database to
multiply agents' scores affects their selection of those plans. This
value can be considered to be a scaling function, which maps utility
in Euro to unit-less values for the logit selection. In real-world
applications, 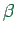 will be estimated together with 36#32,
38#34, and
will be estimated together with 36#32,
38#34, and
 . This paper uses a value of
42#38
as a baseline value, and then looks at deviations from
that value in Sec. 5.4. In estimated multinomial
logit models, it seems that values between 43#39 and
44#40
are normal.
. This paper uses a value of
42#38
as a baseline value, and then looks at deviations from
that value in Sec. 5.4. In estimated multinomial
logit models, it seems that values between 43#39 and
44#40
are normal.


Next: Results
Up: An Improved Framework for
Previous: Implementation of the framework
2004-05-09
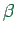 is a constant (see
below). This is just a standard multinomial logit model
(e.g. 5).
is a constant (see
below). This is just a standard multinomial logit model
(e.g. 5).
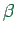 affects how likely agents choose ``non-best''
plans. Higher values of
affects how likely agents choose ``non-best''
plans. Higher values of 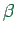 lead toward the best plan being
chosen more often, while smaller values provide a more randomized
choice. Since
lead toward the best plan being
chosen more often, while smaller values provide a more randomized
choice. Since 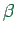 interacts with the scaling of the scoring
function, it is discussed in more detail there.
interacts with the scaling of the scoring
function, it is discussed in more detail there.