


Next: Interpretation as dynamical system
Up: Learning and feedback
Previous: Additional aspects of day-to-day
Contents
Subsections
Individualization of knowledge
Knowledge of agents should be private, i.e. each agent should have a
different set of knowledge items. For example, people typically only
know a relatively small subset of the street network (``mental map''),
and they have different knowledge and perception of congestion. This
suggests the use of Complex Adaptive Systems methods (e.g.
(56)). Here, each agent has a set of strategies from
which to choose, and indicators of past performance for these
strategies. The agent normally choses a well-performing strategy.
From time to time, the agent choses one of the other strategies, to
check if its performance is still bad, or replaces a bad strategy by a
new one.
This approach divides the problem into three parts (see
also (14)):
- Generation of new options. Here new options are generated.
- Evaluation. Here, plans (or strategies) are
evaluated. In our context this means that travelers try out all
their different strategies, and the strategies obtain scores.
- Exploitation. Eventually, the agents settle down on the
better-performing strategies.
As usual, the challenge is to balance exploration (including
generation) and exploitation. This is particularly problematic here
because of the co-evolution aspect: If too many agents do exploration,
then the system performance is not representative of a ``normal''
performance, and the exploring agents do not learn anything at all.
If, however, they explore too little, the system will relax too slowly
(cf. ``run 4'' and ``run 5'' in Fig. 31.1). We have good
experiences with the following scheme:
- A randomly selected 10% of the population obtains new options,
and tries them out immediately in the following simulation run.
- All other travelers choose between their existing options, where
the probability of selecting option
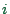 is taken as
is taken as
 |
(31.1) |
where 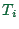 is the remembered travel time for that option.
is the remembered travel time for that option. 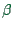 was taken as
was taken as 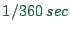 , which lead (in the scenario that was used)
to another 10% of travelers not selecting the optimal option.
, which lead (in the scenario that was used)
to another 10% of travelers not selecting the optimal option.
A major advantage of this approach is that it becomes more robust
against artifacts of the router: if an implausible route is generated,
the simulation as a whole will fall back on a more plausible route
generated earlier. Fig. 31.2 shows an example. The
scenario is the same as in Fig. 2.4 of
Chap. 2; the location is slightly north of the final
destination of all trips. We see snapshots of two relaxed scenarios.
The left plot was generated with a standard relaxation method as
described in the previous section, i.e. where individual travelers
have no memory of previous routes and their performance. The right
plot in contrast was obtained from a relaxation method which uses
exactly the same router but which uses an agent data base,
i.e. it retains memory of old options. In the left plot, we see that
many vehicles are jammed up on the side roads while the freeway is
nearly empty, which is clearly implausible; in the right plot, we see
that at the same point in time, the side roads are empty while the
freeway is just emptying out - as it should be.
The reason for this behavior is that the router miscalculates at which
time it expects travelers to be at certain locations - specifically,
it expects travelers to be much earlier at the location shown in the
plot. In consequence, the router ``thinks'' that the freeway is
heavily congested and thus suggests the side road as an alternative.
Without an agent data base, the method forces the travelers to use
this route; with an agent data base, agents discover that it is faster
to use the freeway.
This means that now the true challenge is not to generate exactly the
correct routes, but to generate a set of routes which is a superset of
the correct ones (14). Bad routes will be weeded
out via the performance evaluation method. For more details see
(). Other implementations of partial aspects
are (124,116,115,51).
The way we have explained it, each individual needs computational
memory to store his/her plan or plans. The memory requirements for
this are of the order of
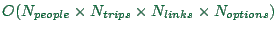 , where
, where 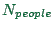 is the number of
people in the simulation,
is the number of
people in the simulation, 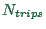 is the number of trips a person
takes per day,
is the number of trips a person
takes per day, 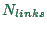 is the average number of links between
starting point and destination, and
is the average number of links between
starting point and destination, and 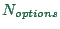 is the number of
options remembered per agent. For example, for a 24-hour simulation
of all traffic in Switzerland, we have
is the number of
options remembered per agent. For example, for a 24-hour simulation
of all traffic in Switzerland, we have
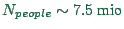 ,
,
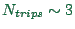 ,
,
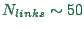 , and
, and
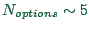 , which results in
, which results in
 |
(31.2) |
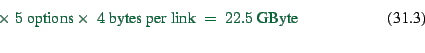 |
(31.3) |
of storage if we use 4-byte words for storage of integer numbers. Let
us call this agent-oriented plans storage.
Since this is a large storage requirement, many approaches do not
store plans in this way. They store instead the shortest path for
each origin-destination combination. This becomes affordable since
one can organize this information in trees anchored at each possible
destination. Each intersections has a ``signpost'' which gives, for
each destination, the right direction; a plan is thus given by knowing
the destination and following the ``signs'' at each intersection. The
memory requirements for this are of the order of
 , where
, where  is the number
of nodes of our network, and
is the number
of nodes of our network, and
 is the number of
possible destinations.
is the number of
possible destinations. 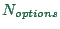 is again the number of options,
but note that these are options per destination, so different
agents traveling to the same destination cannot have more than
is again the number of options,
but note that these are options per destination, so different
agents traveling to the same destination cannot have more than
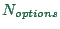 different options between them.
different options between them.
Traditionally, transportation simulations use of
the order of 1000 destination zones, and networks with of the
order of 10000 nodes, which results in a memory requirement of
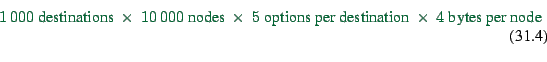 |
(31.4) |
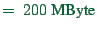 , considerable less than above. Let us call this
network-oriented plans storage.
, considerable less than above. Let us call this
network-oriented plans storage.
The problem with this second approach is that it explodes with more
realistic representations. For example, for our simulations we
usually replace the traditional destinations zones by the links, i.e.
each of typically 30000 links is a possible destination. In
addition, we need the information time-dependent. If we assume that
we have 15-min time slices, this results in a little less than
100 time slices for a full day.
The memory requirements for the second method now become
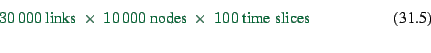 |
(31.5) |
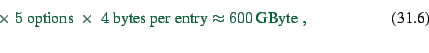 |
(31.6) |
already more than for the agent-oriented approach. In contrast, for
agent-oriented plans storage, time resolution has no effect. The situation
becomes worse with high resolution networks (orders of magnitude more
links and nodes), which leaves the agent-oriented approach nearly
unaffected while the network-oriented approach becomes impossible. As
a side remark, we note that in both cases it is possible to compress
plans by a factor of at least 30 (21).
Figure 31.2:
Individualization of plans and interaction with router
artifacts. LEFT: All vehicles are re-planned according to the
same information; vehicles do not use the freeway (arrrows)
although the freeway is empty. As explained in the text, this
happens because the router makes erroneous predictions about
where a vehicle will be at what time.
RIGHT: Vehicles treat routing results as additional options,
that is, they can revert to other (previously used) options. As
a result, the side road now empty out before the freeway. -
The time is 7pm.
|
|



Next: Interpretation as dynamical system
Up: Learning and feedback
Previous: Additional aspects of day-to-day
Contents
2004-02-02


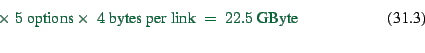
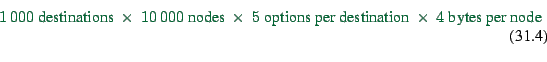
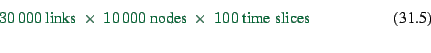
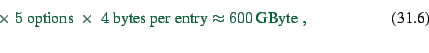
![\includegraphics[width=0.7\hsize]{gz/individualization.eps.gz}](img733.png)