

Next: Future Plans
Up: Large scale multi-agent simulations
Previous: A Practical Scenario
Subsections
Computational Aspects
Computational performance of the mobility simulation
It is possible to make the mobility simulation parallel, i.e. to give
different pieces of it to different CPUs (Central Processing Units).
One good option is to do
this via domain decomposition; that is, the geographical area is
decomposed into domains, and each CPU computes traffic within that
domain. These domains need to exchange information at their borders,
which can be achieved by messages. For messages, existing message
passing software such as MPI (Message Passing Interface,
www.mcs.anl.gov/mpi/) or PVM (Parallel Virtual Machine,
www.epm.ornl.gov/pvm) can be used.
In this situation, simulation time per time step is a sum of the time
spent on computation and the time spent on communication,
where 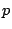 is the number of CPUs. For the purposes of an intuitive
understanding, let us assume that
is the number of CPUs. For the purposes of an intuitive
understanding, let us assume that
i.e. that there is a true distribution of work. 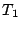 is the time a
single CPU needs. For the communication, it turns out that the main
component is the latency
is the time a
single CPU needs. For the communication, it turns out that the main
component is the latency 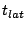 of the communication. Latency
refers to the amount of time that is necessary to prepare a message
before it can be sent away. Most of that time is caused by the
hardware, such as Ethernet, and the corresponding Internet protocols,
such as TCP/IP. For 100 Mbit Ethernet, this latency time is of the
order of
of the communication. Latency
refers to the amount of time that is necessary to prepare a message
before it can be sent away. Most of that time is caused by the
hardware, such as Ethernet, and the corresponding Internet protocols,
such as TCP/IP. For 100 Mbit Ethernet, this latency time is of the
order of 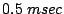 . Since in two-dimensional systems each domain has
in the average six neighbors, and we need two messages per time step,
communication time can be approximated as
. Since in two-dimensional systems each domain has
in the average six neighbors, and we need two messages per time step,
communication time can be approximated as
Overall, this results in
Let us define the real time ratio as how much faster than
reality the simulation is. If we assume that one simulation time step
corresponds to one second, then we obtain
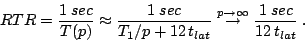 |
(2) |
For 100 Mbit Ethernet,
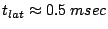 , and therefore
, and therefore 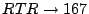 for
for 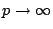 . In words:
This statement is independent of the problem size or of the specific
model, it only depends on the fact that a simulation time-step
corresponds to one second.
. In words:
This statement is independent of the problem size or of the specific
model, it only depends on the fact that a simulation time-step
corresponds to one second.
The actual performance measurements in Fig. 5(a) from our
implementation (dots) demonstrate that these concerns are justified.
The line is a fit to those performance measurements, based on the
mathematical form of Eq. (2). The results of
Fig. 5 refer to runs of the Switzerland 6-9 scenario
as explained above. Only with a faster communication hardware,
Myrinet (www.myri.com), this bottleneck can be overcome and much
faster simulations can be achieved. Our best performance currently is
an RTR of nearly 800. This means that a whole day of all car traffic
in Switzerland, which has about 7 mio inhabitants, can be simulated in
less than 2 minutes. This makes now large scale learning studies
possible, although it should be noted that these performance numbers
are obtained without taking data input and output into account.
Fig. 5(b) also shows the speedup for the same runs.
Speedup is defined as the performance ratio between a multi-CPU and a
single-CPU run:
As one can see in the plots, speedup is obtained by shifting the RTR
curve vertically; the amount of shifting is given by the RTR of the
single-CPU run.
As one sees, our fastest simulation is, on 64 CPUs, about 200 times
faster than the single-CPU simulation. This so-called super-linear
speedup is caused by the fact that the scenario is too large to fit
comfortably into a single-CPU machine and thus causes slow memory
paging there. Without further information, speedup curves cannot be
used to understand real time limitations on the computation, which is
important for ITS applications. - More information can be found in
Cetin and Nagel (15).
Figure 5:
(a) RTR and (b) Speedup curves of the ch6-9 scenario
from Feb 2003, with the default domain decomposition approach. Dots
refer to actual computational benchmarks; the solid line is based on the
theory explained in the text.
Feb 2003:
[]
![\includegraphics[width=0.5\hsize]{rtr-gpl.eps}](img58.png) []
![\includegraphics[width=0.5\hsize]{speedup-gpl.eps}](img59.png)
|
Figure 6 depicts the cumulative contributions
of the major steps in the feedback system to the total execution time
of each iteration. The left figure shows the implementation of the
feedback mechanism with MySQL (www.mysql.org), a file-based database.
As explained in Sec. 4, the agent database keeps
track of agent strategies and their scores. The right figure shows an
implementation where all relevant data (i.e. strategies) are
permanently kept in computer memory. Rather than using slower
scripting languages for each step in the iteration (48), the
new implementation is written in C++ and combines all operations into
one program. The figure shows computational performance results for
the scenario described in Sec. 5; the contributions
shown in the figure are:
- Strategy Generation adds a new strategy for 10% of the
agents into the database. Once the network data has relaxed, this
step takes about the same amount of time in each iteration.
- Strategy Selection, where the other 90% of the agents
select a strategy from the database.
In the left figure, the execution time for this
step scales approximately linearly with the total number of
strategies stored in the agent database. Thus, it takes longer to
execute with each iteration. In the right figure it takes
essentially the same amount of time in each iteration.
- Mobility Simulation, where the agents interact. This
again relaxes to a consistent amount of time, though takes longer in earlier iterations when there is more
congestion to deal with.
In the left figure, this step ends up taking about 15 minutes
while in the right it ends up taking only about 10 minutes. This is
due to an improvement in the mobility simuation speed between trials,
and has nothing to do with the agent database.
- Score Update, where the agents update the performance
scores of their executed strategy from the output of the mobility
simulation. The execution time for this operation is fairly
constant in each iteration, since it depends on the number of events
produced by the simulation (see Sec. 2).
This number is proportional to the number of agents and the length
of their routes; it does not change very much from one iteration to
the next.
In the left figure, this operation takes about 20 minutes while in
the right figure it takes about 10 minutes.
More details about the database
implementation and execution times can be found in Raney and Nagel (48).
One can see that
in the left figure,
on average each iteration takes about an hour to
execute, with the feedback system, with strategy-related steps
totaling about 45 minutes of that time. The overall result is that we
can run a metropolitan scenario with 1 million agents, including 50
learning iterations, in about two days.
For the right figure, the total time is cut in half, with about
20 minutes spent on strategy-related steps.
Figure 6:
Cumulative Execution Time Contributions of Major Iteration Steps
LEFT: File-based database implementation.
RIGHT: The new implementation, which keeps all agent information in
computer memory, and which also uses a faster mobility simulation.
|
|


Next: Future Plans
Up: Large scale multi-agent simulations
Previous: A Practical Scenario
2004-05-09
![\fbox{%%
\begin{minipage}[c]{0.9\hsize}
\emph{With 100~Mbit Ethernet, the best p...
...ic simulation with a one-second time step is
approximately 170.}
\end{minipage}}](img56.png)
![\includegraphics[width=0.5\hsize]{rtr-gpl.eps}](img58.png) []
[]
![\includegraphics[width=0.5\hsize]{speedup-gpl.eps}](img59.png)
![\includegraphics[width=0.49\hsize]{db_execution_time-gpl.eps}](img60.png)
![\includegraphics[width=0.49\hsize]{brain_execution_time-gpl.eps}](img61.png)