It is possible to systematically predict the performance of parallel micro-simulations (e.g. (86,58)). For this, several assumptions about the computer architecture need to be made. In the following, we demonstrate the derivation of such predictive equations for coupled workstations and for parallel supercomputers.
The method for this is to systematically calculate the wall clock time
for one time step of the micro-simulation. We start by assuming that
the time for one time step has contributions from computation,
![]() , and from communication,
, and from communication, ![]() . If these do not
overlap, as is reasonable to assume for coupled workstations, we have
. If these do not
overlap, as is reasonable to assume for coupled workstations, we have
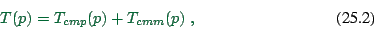 |
(25.2) |
Time for computation is assumed to follow
Time for communication typically has two contributions: Latency and
bandwidth. Latency is the time necessary to initiate the
communication, and in consequence it is independent of the message
size. Bandwidth describes the number of bytes that can be
communicated per second. So the time for one message is

However, for many of today's computer architectures, bandwidth is given by at least two contributions: node bandwidth, and network bandwidth. Node bandwidth is the bandwidth of the connection from the CPU to the network. If two computers communicate with each other, this is the maximum bandwidth they can reach. For that reason, this is sometimes also called the ``point-to-point'' bandwidth.
The network bandwidth is given by the technology and topology of the network. Typical technologies are 10 Mbit Ethernet, 100 Mbit Ethernet, FDDI, etc. Typical topologies are bus topologies, switched topologies, two-dimensional topologies (e.g. grid/torus), hypercube topologies, etc. A traditional Local Area Network (LAN) uses 10 Mbit Ethernet, and it has a shared bus topology. In a shared bus topology, all communication goes over the same medium; that is, if several pairs of computers communicate with each other, they have to share the bandwidth.
For example, in our 100 Mbit FDDI network (i.e. a network bandwidth
of ![]() Mbit) at Los Alamos National Laboratory, we found
node bandwidths of about
Mbit) at Los Alamos National Laboratory, we found
node bandwidths of about ![]() Mbit. That means that two
pairs of computers could communicate at full node bandwidth, i.e.
using 80 of the 100 Mbit/sec, while three or more pairs were limited
by the network bandwidth. For example, five pairs of computers could
maximally get
Mbit. That means that two
pairs of computers could communicate at full node bandwidth, i.e.
using 80 of the 100 Mbit/sec, while three or more pairs were limited
by the network bandwidth. For example, five pairs of computers could
maximally get ![]() Mbit/sec each.
Mbit/sec each.
A switched topology is similar to a bus topology, except that the network bandwidth is given by the backplane of the switch. Often, the backplane bandwidth is high enough to have all nodes communicate with each other at full node bandwidth, and for practical purposes one can thus neglect the network bandwidth effect for switched networks.
If computers become massively parallel, switches with enough backplane
bandwidth become too expensive. As a compromise, such supercomputers
usually use a communications topology where communication to
``nearby'' nodes can be done at full node bandwidth, whereas global
communication suffers some performance degradation. Since we
partition our traffic simulations in a way that communication is
local, we can assume that we do communication with full node bandwidth
on a supercomputer. That is, on a parallel supercomputer, we can
neglect the contribution coming from the ![]() -term. This
assumes, however, that the allocation of street network partitions to
computational nodes is done in some intelligent way which maintains
locality.
-term. This
assumes, however, that the allocation of street network partitions to
computational nodes is done in some intelligent way which maintains
locality.
As a result of this discussion, we assume that the communication
time per time step is
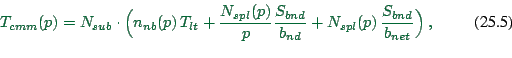
![]() is the number of neighbor domains each CPU talks to. All
information which goes to the same CPU is collected and sent as a
single message, thus incurring the latency only once per neighbor
domain. For
is the number of neighbor domains each CPU talks to. All
information which goes to the same CPU is collected and sent as a
single message, thus incurring the latency only once per neighbor
domain. For ![]() ,
, ![]() is zero since there is no other domain to
communicate with. For
is zero since there is no other domain to
communicate with. For ![]() , it is one. For
, it is one. For ![]() and
assuming that domains are always connected, Euler's theorem for planar
graphs says that the average number of neighbors cannot become more
than six. Based on a simple geometric argument, we use
and
assuming that domains are always connected, Euler's theorem for planar
graphs says that the average number of neighbors cannot become more
than six. Based on a simple geometric argument, we use
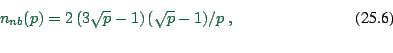
![]() is the latency (or start-up time) of each message.
is the latency (or start-up time) of each message. ![]() between 0.5 and 2 milliseconds are typical values for PVM on a
LAN (39,100).
between 0.5 and 2 milliseconds are typical values for PVM on a
LAN (39,100).
Next are the terms that describe our two bandwidth effects.
![]() is the number of split links in the whole simulation;
this was already discussed in Sec. 25.3 (see
Fig. 25.5). Accordingly,
is the number of split links in the whole simulation;
this was already discussed in Sec. 25.3 (see
Fig. 25.5). Accordingly, ![]() is the number
of split links per computational node.
is the number
of split links per computational node. ![]() is the size of
the message per split link.
is the size of
the message per split link. ![]() and
and ![]() are the
node and network bandwidths, as discussed above.
are the
node and network bandwidths, as discussed above.
In consequence, the combined time for one time step is
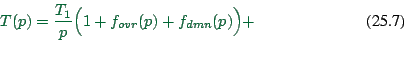
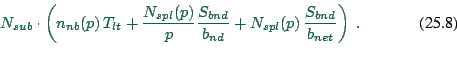
According to what we have discussed above, for ![]() the
number of neighbors scales as
the
number of neighbors scales as
![]() and the number of
split links in the simulation scales as
and the number of
split links in the simulation scales as
![]() . In consequence for
. In consequence for ![]() and
and ![]() small enough,
we have:
small enough,
we have:
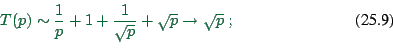
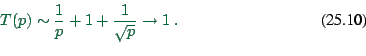
The curves in Fig. 25.10 are results from this
prediction for a switched 100 Mbit Ethernet LAN; dots and crosses show
actual performance results. The top graph shows the time for one time
step, i.e. ![]() , and the individual contributions to this value.
The bottom graph shows the real time ratio (RTR)
, and the individual contributions to this value.
The bottom graph shows the real time ratio (RTR)
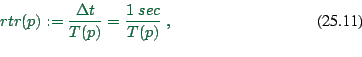
The plot (Fig. 25.10) shows that even something as relatively profane as a combination of regular Pentium CPUs using a switched 100Mbit Ethernet technology is quite capable in reaching good computational speeds. For example, with 16 CPUs the simulation runs 40 times faster than real time; the simulation of a 24 hour time period would thus take 0.6 hours. These numbers refer, as said above, to the Portland 20024 links network. Included in the plot (black dots) are measurements with a compute cluster that corresponds to this architecture. The triangles with lower performance for the same number of CPUs come from using dual instead of single CPUs on the computational nodes. Note that the curve levels out at about forty times faster than real time, no matter what the number of CPUs. As one can see in the top figure, the reason is the latency term, which eventually consumes nearly all the time for a time step. This is one of the important elements where parallel supercomputers are different: For example the Cray T3D has a more than a factor of ten lower latency under PVM (39).
As mentioned above, we also ran the same simulation without any vehicles. In the Transims1999 implementation, the simulation sends the contents of each CA boundary region to the neighboring CPU even when the boundary region is empty. Without compression, this is five integers for five sites, times the number of lanes, resulting in about 40 bytes per split edge, which is considerably less than the 800 bytes from above. The results are shown in Fig. 25.11. Shown are the computing times with 1 to 15 single-CPU slaves, and the corresponding real time ratio. Clearly, we reach better speed-up without vehicles than with vehicles (compare to Fig. 25.10). Interestingly, this does not matter for the maximum computational speed that can be reached with this architecture: Both with and without vehicles, the maximum real time ratio is about 80; it is simply reached with a higher number of CPUs for the simulation with vehicles. The reason is that eventually the only limiting factor is the network latency term, which does not have anything to do with the amount of information that is communicated.
Fig. 25.12 (top) shows some predicted real time ratios for other computing architectures. For simplicity, we assume that all of them except for one special case explained below use the same 500 MHz Pentium compute nodes. The difference is in the networks: We assume 10 Mbit non-switched, 10 Mbit switched, 1 Gbit non-switched, and 1 Gbit switched. The curves for 100 Mbit are in between and were left out for clarity; values for switched 100 Mbit Ethernet were already in Fig. 25.10. One clearly sees that for this problem and with today's computers, it is nearly impossible to reach any speed-up on a 10 Mbit Ethernet, even when switched. Gbit Ethernet is somewhat more efficient than 100 Mbit Ethernet for small numbers of CPUs, but for larger numbers of CPUs, switched Gbit Ethernet saturates at exactly the same computational speed as the switched 100 Mbit Ethernet. This is due to the fact that we assume that latency remains the same - after all, there was no improvement in latency when moving from 10 to 100 Mbit Ethernet. FDDI is supposedly even worse (39).
The thick line in Fig. 25.12 corresponds to the ASCI Blue Mountain parallel supercomputer at Los Alamos National Laboratory. On a per-CPU basis, this machine is slower than a 500 MHz Pentium. The higher bandwidth and in particular the lower latency make it possible to use higher numbers of CPUs efficiently, and in fact one should be able to reach a real time ratio of 128 according to this plot. By then, however, the granularity effect of the unequal domains (Eq. (25.1), Fig. 25.7) would have set in, limiting the computational speed probably to about 100 times real time with 128 CPUs. We actually have some speed measurements on that machine for up to 96 CPUs, but with a considerably slower code from summer 1998. We omit those values from the plot in order to avoid confusion.
Fig. 25.12 (bottom) shows predictions for the higher
fidelity Portland 200000 links network with the same
computer architectures. The assumption was that the time for one time
step, i.e. ![]() of Eq. (25.3), increases by a factor of
eight due to the increased load. This has not been verified yet.
However, the general message does not depend on the particular
details: When problems become larger, then larger numbers of CPUs
become more efficient. Note that we again saturate, with the switched
Ethernet architecture, at 80 times faster than real time, but this
time we need about 64 CPUs with switched Gbit Ethernet in order to get
40 times faster than real time -- for the smaller Portland
20024 links network with switched Gbit Ethernet we would
need 8 of the same CPUs to reach the same real time ratio. In short
and somewhat simplified: As long as we have enough CPUs, we can
micro-simulate road networks of arbitrarily largesize, with
hundreds of thousands of links and more, 40 times faster than real
time, even without supercomputer hardware. -- Based on our
experience, we are confident that these predictions will be lower
bounds on performance: In the past, we have always found ways to make
the code more efficient.
of Eq. (25.3), increases by a factor of
eight due to the increased load. This has not been verified yet.
However, the general message does not depend on the particular
details: When problems become larger, then larger numbers of CPUs
become more efficient. Note that we again saturate, with the switched
Ethernet architecture, at 80 times faster than real time, but this
time we need about 64 CPUs with switched Gbit Ethernet in order to get
40 times faster than real time -- for the smaller Portland
20024 links network with switched Gbit Ethernet we would
need 8 of the same CPUs to reach the same real time ratio. In short
and somewhat simplified: As long as we have enough CPUs, we can
micro-simulate road networks of arbitrarily largesize, with
hundreds of thousands of links and more, 40 times faster than real
time, even without supercomputer hardware. -- Based on our
experience, we are confident that these predictions will be lower
bounds on performance: In the past, we have always found ways to make
the code more efficient.
![\includegraphics[width=0.8\hsize]{cars-time-gpl.eps}](img310.png)
![\includegraphics[width=0.8\hsize]{cars-rtr-gpl.eps}](img311.png)
|
![\includegraphics[width=0.8\hsize]{nocars-time-gpl.eps}](img312.png)
![\includegraphics[width=0.8\hsize]{nocars-rtr-gpl.eps}](img313.png)
|
![\includegraphics[width=0.7\hsize]{other-rtr-gpl.eps}](img314.png)
![\includegraphics[width=0.7\hsize]{ten-rtr-gpl.eps}](img315.png)
|